11.1. (Exercise) Introduction to Hybrid models. Combining Physics-Based and Machine Learning Models#
11.1.1. Learning Objectives:#
How can we model glaciers with physic-based approach?
Understand what hybrid models are and how they integrate physics-based and ML approaches.
Explore the advantages and shortcomings of using hybrid models.
Examine different applications for combining machine learning and physical models.
Q: According to you, what is a glacier ?
To me : A glacier is a non-Newtonian fluid, with a stress dependent viscosity, that flows from higher to lower elevations
11.1.1.1. Introduction to Glacier Flow#
Glaciers are massive bodies of ice that flow slowly under their own weight. The flow of ice in a glacier is a complex process governed by physical laws that describe how the ice deforms and moves. Given an initial glacier geometry, the time evolution in ice thickness \(h(x, y, t)\) is determined by the mass conservation equation, which couples ice dynamics and surface mass balance (SMB) through:
\( \begin{aligned} \frac{\partial h}{\partial t} + \nabla \cdot (\mathbf{u}h) = SMB, \\ \end{aligned} \)
where \(\nabla \cdot\) denotes the divergence operator with respect to the flux (\(Q=\mathbf{u}h\)). \(\mathbf{u}\) is the vertically averaged horizontal ice velocity field and SMB the SMB function, which consists of the integration of ice accumulation and ablation over one year.
Mass conservation equation is generic and can be applied to model glacier evolution in number of applications provided adequate SMB and ice-flow model components. In the following, we mostly focus on developing an efficient numerical method to compute the ice-flow considering it is often the most computationally expensive component in glacier evolution model.
First, we will use a numerical solution to compute \(Q\).
Then we will use a data-driven Machine Learning (ML) approach that emulates ice-flow. The state of the art ML techniques, use a Physics Informed Neural Network (PINN); however, this goes beyond the scope of this chapter which focuses on hybrid models.
11.1.1.2. Numerical solution for u#
We can describe the ice-flow equations under stress, but their computational cost makes them impractical for large-scale ice-sheet modeling over long time periods. This leads us to introduce the shallow ice approximation (SIA), which is used in ice sheet models due to its simplicity and efficiency.
The SIA simplifies the full Stokes equations by assuming that the ice flow is dominated by vertical shear stresses and that horizontal stresses can be neglected. This results in an expression for the ice velocity in terms of the ice thickness gradient and the surface slope. The ice velocity \(\mathbf{u}\) can be approximated as:
\( \mathbf{u} = -\left(\frac{2 A}{n+2}\right) \left(\rho g \sin(s)\right)^n h^{n+1} \nabla h, \)
where:
\(\rho\) is the ice density,
\(g\) is the gravitational acceleration,
\(A\) is Glen’s flow rate factor,
\(n\) is Glen’s law exponent (typically 3),
\(h\) is the ice thickness, and
\(s\) is the surface slope.
This equation governs the horizontal velocity of ice based on the local ice thickness and slope. We plug the u into the mass conservation equation and obtain:
\( \frac{\partial h}{\partial t} + \nabla \cdot (D(h,z)\frac{\partial z}{\partial x}) = \text{SMB}, \)
where \(D(h,z) = f_d (\rho g)^3 h^5 |\nabla S|^2\).
This equation describes the time evolution of the ice thickness, where the velocity \(\mathbf{u}\) is computed from the ice sheet’s surface slope and thickness. This approach provides a balance between accuracy and computational efficiency and is widely used in large-scale ice sheet models.
11.1.1.2.1. Boundary Conditions with no-slip condition at the case#
In many glacier models, we assume a no-slip condition at the base, meaning the ice velocity is zero at the bedrock. This condition is suitable for glaciers frozen to their beds:
\( \mathbf{u} = 0 \text{ on the bedrock surface}. \)
Stress-Free Surface
At the glacier surface (exposed to air), a stress-free boundary condition is typically applied:
\( \sigma \cdot \mathbf{n} = 0 \text{ on the surface}, \)
Where \(\mathbf{n}\) is the outward normal vector at the glacier surface.
#import the necessary libraies
import numpy as np
import matplotlib.pyplot as plt
from scipy import ndimage
import netCDF4
from IPython.display import clear_output
import pooch
import xarray as xr
import tensorflow as tf
from tensorflow.keras.models import load_model
# Make True if you want to train the model from scratch. It should take 30 min to train.
train_mode=True
%matplotlib inline
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Cell In[1], line 5
3 import matplotlib.pyplot as plt
4 from scipy import ndimage
----> 5 import netCDF4
6 from IPython.display import clear_output
7 import pooch
ModuleNotFoundError: No module named 'netCDF4'
# Physical parameters
Lx = 49700 # Domain length in x (m)
Ly = 32300 # Domain length in y (m)
ttot = 700 # Time limit (yr)
grad_b = 0.001 # Mass balance gradient (no unit)
b_max = 0.5 # Maximum precip (m/yr)
Z_ELA = 3000 # Elevation of equilibrium line altitude (m)
rho = 910.0 # Ice density (g/m^3)
g = 9.81 # Earth's gravity (m/s^2)
fd = 1e-18 # Deformation constant (Pa^-3 y^-1)
# Initialization & load data
nout = 50 # Frequency of plotting
dtmax = 1 # maximum time step
dt = dtmax # Initial time step
dx = 100
dy = 100 # Cell size in y
nx=int(Lx/dx)
ny=int(Ly/dy)
x = np.linspace(0, Lx, nx) # x-coordinates
y = np.linspace(0, Ly, ny) # y-coordinates
bedrock_url='https://unils-my.sharepoint.com/:u:/g/personal/kejdi_lleshi_unil_ch/EXI_z9iu_MlMn_J4IdG97DkBpvE8K-IKiZUxuEogU-cwVg?download=1'
hash = None
file = pooch.retrieve(bedrock_url, known_hash=hash)
nc_file = netCDF4.Dataset(file) # Load the NetCDF file
Z_topo = nc_file.variables['topg'] # Replace 'topg' with the appropriate v
H_ice = np.zeros((ny, nx)) # Initial ice thickness
Z_surf = Z_topo + H_ice # Initial ice surface
time = 0 # Initial time
it = 0
# Loop
while time < ttot:
# Update time
time += dt
it += 1
# Calculate H_avg, size (ny-1,nx-1)
H_avg = 0.25 * (H_ice[:-1, :-1] + H_ice[1:, 1:] + H_ice[:-1, 1:] + H_ice[1:, :-1])
# Compute Snorm, size (ny-1,nx-1)
Sx = np.diff(Z_surf, axis=1) / dx
Sy = np.diff(Z_surf, axis=0) / dy
Sx = 0.5 * (Sx[:-1, :] + Sx[1:, :])
Sy = 0.5 * (Sy[:, :-1] + Sy[:, 1:])
Snorm = np.sqrt(Sx**2 + Sy**2)
# Compute D, size (ny-1,nx-1)
D = fd * (rho * g)**3.0 * H_avg**5 * Snorm**2
# Compute dt
dt = min(min(dx, dy)**2 / (4.1 * np.max(D)), dtmax)
# Compute qx, size (ny-2,nx-1)
qx = -(0.5 * (D[:-1,:] + D[1:,:])) * np.diff(Z_surf[1:-1,:], axis=1) / dx
# Compute qy, size (ny-1,nx-2)
qy = -(0.5 * (D[:,:-1] + D[:,1:])) * np.diff(Z_surf[:,1:-1,], axis=0) / dy
# Update rule (diffusion)
dHdt = -(np.diff(qx, axis=1) / dx + np.diff(qy, axis=0) / dy)
H_ice[1:-1, 1:-1] += dt * dHdt # size (ny-2,nx-2)
b = np.minimum(grad_b * (Z_surf - Z_ELA), b_max)
# Update rule (mass balance)
H_ice[1:-1, 1:-1] += dt * b[1:-1, 1:-1]
# Update rule (positive thickness)
H_ice = np.maximum(H_ice, 0)
# updatesurface topography
Z_surf = Z_topo + H_ice
# Update ELA after 500 years
if time > 500:
Z_ELA = 2700
# Display
if it % nout == 0:
clear_output(wait=True) # Clear the previous output in the notebook
plt.figure(2, figsize=(11, 4), dpi=200)
# First subplot: Ice surface
plt.subplot(1, 2, 1)
plt.imshow(Z_surf, extent=[0, Lx/1000, 0, Ly/1000], cmap='terrain', origin='lower')
plt.colorbar(label='Elevation (m)')
plt.title('Ice Surface at ' + str(int(time)) + ' y')
plt.xlabel('Distance, km')
plt.ylabel('Distance, km')
# Second subplot: Ice thickness
plt.subplot(1, 2, 2)
plt.imshow(np.where(H_ice > 0, H_ice, np.nan), extent=[0, Lx/1000, 0, Ly/1000], cmap='jet', origin='lower')
plt.colorbar(label='Ice Thickness (m)')
plt.title('Ice Thickness at ' + str(int(time)) + ' y')
plt.xlabel('Distance, km')
plt.ylabel('Distance, km')
# Show the plot
plt.show()
Q: Which is the most expensive part of of solving the mass conservation equation?
The most expensive part is the calculation of u.
11.1.2. Introduction to hybrid modeling#
Hybrid models combine traditional physics-based models (model-based, MB) with machine learning (ML) to leverage the strengths of both approaches. In purely physics-based models, known equations govern system dynamics, but these models often require detailed domain knowledge and can be limited by the availability of precise parameters. Machine learning, in contrast, can model complex systems without relying on such parameters, making it useful for data-rich but theory-poor domains. However, ML models may struggle to generalize outside the data they are trained on and can produce results that violate known physical laws.
Q: How can hybrid models overcome these limitations?
Hybrid modeling overcomes these limitations by using physics-informed constraints, embedding known physical equations into machine learning models, or combining the outputs of both approaches. The goal is to create models that are more accurate and robust, especially in cases with limited data or imperfect physical models. By fusing physics with data-driven methods, hybrid models can handle sparse data, correct ML predictions that violate physical laws, and produce interpretable results across a wide range of applications.
Q: How can we make our simulations run faster?
We can replace the calutation of u with an emulator. The emulator will take as input the state of the medium (glacier thickness, slope of glacier, etc) and will calucate the velocity field (u) for the corresponding time step.
11.1.2.1. Emulating Ice Flow with Machine Learning#
The Instructed Glacier Model (IGM) introduces a convolutional neural network (CNN) to predict ice flow, trained using data from traditional models such as hybrid SIA+SSA or Stokes models. The advantage of this approach is that it substitutes the computationally expensive ice flow component with a much faster emulator. This enables simulations that are up to 1000 times faster, with a fidelity of over 90%.
11.1.2.1.1. Overview of the Machine Learning Approach#
A simple version of the IGM could be built by the following steps:
Input Variables: The ML model takes ice thickness and surface slope gradients as inputs \(\{ h(x,y), \frac{\partial s}{\partial x},\frac{\partial s}{\partial y}\}\).
Training: A convolutional neural network (CNN) is trained using a dataset generated from high-order glacier flow models.
Prediction: Once trained, the emulator predicts the vertically averaged ice flow from the input variables u(u,v).
The input and output fields are 2 D grid rasters:
\( \R^{N_x \times N_y \times 3} \rightarrow \R^{N_x \times N_y \times 2} , \)
Q: what is another advantage of the hybrid model (except making faster models)?
Hybrid models can help in theory-poor domains where we do not have known equation that govern system dynamics. However, we should have enough data and be sure to make this model generalizable. A pitfall, when we dont have enough data and are not carefull, could be to overfitting
11.1.2.1.2. Necessary funcitons you do not need to know#
#@markdown Test
# Function to load NetCDF files
def load_from_pooch(file):
nc_file = xr.open_dataset(file)
return nc_file
# Function to scale the field based on 90th percentile of its maximum
def scale_field(field):
max_90th_percentile = np.percentile(field.max(axis=(1, 2)), 90)
return field / max_90th_percentile
# Function to augment the data by flipping and adding noise
def augment_data(inputs, outputs):
aug_inputs, aug_outputs = [], []
for inp, out in zip(inputs, outputs):
# Original data
aug_inputs.append(inp)
aug_outputs.append(out)
# Horizontal flip
aug_inputs.append(np.flip(inp, axis=2)) # Flip along x-axis
aug_outputs.append(np.flip(out, axis=2))
# Vertical flip
aug_inputs.append(np.flip(inp, axis=1)) # Flip along y-axis
aug_outputs.append(np.flip(out, axis=1))
return np.array(aug_inputs), np.array(aug_outputs)
# Plot input and output fields side by side with color bars
def plot_input_output(thk, slopesurx, slopesury, ubar, vbar):
fig, axs = plt.subplots(2, 3, figsize=(12, 5))
# Plot inputs
im0 = axs[0, 0].imshow(thk, cmap='Blues')
axs[0, 0].set_title('Ice Thickness (thk)')
axs[0, 0].set_xlabel('x')
axs[0, 0].set_ylabel('y')
fig.colorbar(im0, ax=axs[0, 0], orientation='vertical')
im1 = axs[0, 1].imshow(slopesurx, cmap='RdBu')
axs[0, 1].set_title('Surface Slope x (slopesurx)')
axs[0, 1].set_xlabel('x')
axs[0, 1].set_ylabel('y')
fig.colorbar(im1, ax=axs[0, 1], orientation='vertical')
im2 = axs[0, 2].imshow(slopesury, cmap='RdBu')
axs[0, 2].set_title('Surface Slope y (slopesury)')
axs[0, 2].set_xlabel('x')
axs[0, 2].set_ylabel('y')
fig.colorbar(im2, ax=axs[0, 2], orientation='vertical')
# Plot outputs
im3 = axs[1, 0].imshow(ubar, cmap='viridis')
axs[1, 0].set_title('Velocity x (ubar)')
axs[1, 0].set_xlabel('x')
axs[1, 0].set_ylabel('y')
fig.colorbar(im3, ax=axs[1, 0], orientation='vertical')
im4 = axs[1, 1].imshow(vbar, cmap='viridis')
axs[1, 1].set_title('Velocity y (vbar)')
axs[1, 1].set_xlabel('x')
axs[1, 1].set_ylabel('y')
fig.colorbar(im4, ax=axs[1, 1], orientation='vertical')
# Adjust layout
plt.tight_layout()
plt.show()
def plot_comparison(thk, slopesurx, slopesury, true_ubar, true_vbar, pred_ubar, pred_vbar, time_idx=0):
fig, axs = plt.subplots(3, 3, figsize=(12, 7))
# Plot inputs with individual color bars
im = axs[0, 0].imshow(thk[time_idx, :, :], cmap='Blues')
axs[0, 0].set_title('Ice Thickness (thk)')
axs[0, 0].set_xlabel('x')
axs[0, 0].set_ylabel('y')
fig.colorbar(im, ax=axs[0, 0])
im = axs[0, 1].imshow(slopesurx[time_idx, :, :], cmap='RdBu')
axs[0, 1].set_title('Surface Slope x (slopesurx)')
axs[0, 1].set_xlabel('x')
axs[0, 1].set_ylabel('y')
fig.colorbar(im, ax=axs[0, 1])
im = axs[0, 2].imshow(slopesury[time_idx, :, :], cmap='RdBu')
axs[0, 2].set_title('Surface Slope y (slopesury)')
axs[0, 2].set_xlabel('x')
axs[0, 2].set_ylabel('y')
fig.colorbar(im, ax=axs[0, 2])
# Determine the shared vmin and vmax for velocity comparisons
vmin_ubar = min(true_ubar.min(), pred_ubar.min())
vmax_ubar = max(true_ubar.max(), pred_ubar.max())
vmin_vbar = min(true_vbar.min(), pred_vbar.min())
vmax_vbar = max(true_vbar.max(), pred_vbar.max())
# Plot true outputs with shared color bars
im_ubar_true = axs[1, 0].imshow(true_ubar[time_idx, :, :], cmap='viridis', vmin=vmin_ubar, vmax=vmax_ubar)
axs[1, 0].set_title('True Velocity x (ubar)')
axs[1, 0].set_xlabel('x')
axs[1, 0].set_ylabel('y')
fig.colorbar(im_ubar_true, ax=axs[1, 0])
im_vbar_true = axs[2, 0].imshow(true_vbar[time_idx, :, :], cmap='viridis', vmin=vmin_vbar, vmax=vmax_vbar)
axs[2, 0].set_title('True Velocity y (vbar)')
axs[2, 0].set_xlabel('x')
axs[2, 0].set_ylabel('y')
fig.colorbar(im_vbar_true, ax=axs[2, 0])
# Plot predicted outputs with the same color scales
im_ubar_pred = axs[1, 1].imshow(pred_ubar[time_idx, :, :], cmap='viridis', vmin=vmin_ubar, vmax=vmax_ubar)
axs[1, 1].set_title('Predicted Velocity x (ubar)')
axs[1, 1].set_xlabel('x')
axs[1, 1].set_ylabel('y')
fig.colorbar(im_ubar_pred, ax=axs[1, 1])
im_vbar_pred = axs[2, 1].imshow(pred_vbar[time_idx, :, :], cmap='viridis', vmin=vmin_vbar, vmax=vmax_vbar)
axs[2, 1].set_title('Predicted Velocity y (vbar)')
axs[2, 1].set_xlabel('x')
axs[2, 1].set_ylabel('y')
fig.colorbar(im_vbar_pred, ax=axs[2, 1])
# Plot difference between true and predicted velocities
im_ubar_diff = axs[1, 2].imshow(true_ubar[time_idx, :, :] - pred_ubar[time_idx, :, :], cmap='RdBu')
axs[1, 2].set_title('Difference Velocity x')
axs[1, 2].set_xlabel('x')
axs[1, 2].set_ylabel('y')
fig.colorbar(im_ubar_diff, ax=axs[1, 2])
im_vbar_diff = axs[2, 2].imshow(true_vbar[time_idx, :, :] - pred_vbar[time_idx, :, :], cmap='RdBu')
axs[2, 2].set_title('Difference Velocity y')
axs[2, 2].set_xlabel('x')
axs[2, 2].set_ylabel('y')
fig.colorbar(im_vbar_diff, ax=axs[2, 2])
# Adjust layout
plt.tight_layout()
plt.show()
11.1.2.1.3. Functions to prepare the data for the model#
def prepare_data (merged_data):
# Step 1: Extract the input and output fields
thk = merged_data['thk'].values # Ice thickness
slopsurfx = merged_data['slopsurfx'].values # Surface slope in x
slopsurfy = merged_data['slopsurfy'].values # Surface slope in y
ubar = merged_data['ubar'].values # Velocity x component
vbar = merged_data['vbar'].values # Velocity y component
usurf = merged_data['usurf'].values
# Calculate 90th percentile scaling factors for training
scaling_factors = {
"thk": np.percentile(thk.max(axis=(1, 2)), 90),
"slopsurfx": np.percentile(slopsurfx.max(axis=(1, 2)), 90),
"slopsurfy": np.percentile(slopsurfy.max(axis=(1, 2)), 90),
"ubar": np.percentile(ubar.max(axis=(1, 2)), 90),
"vbar": np.percentile(vbar.max(axis=(1, 2)), 90)
}
# Step 2: Scale each field using the 90th percentile of its maximum
thk_scaled = scale_field(thk)
slopsurfx_scaled = scale_field(slopsurfx)
slopsurfy_scaled = scale_field(slopsurfy)
ubar_scaled = scale_field(ubar)
vbar_scaled = scale_field(vbar)
usurf_scaled = scale_field(usurf)
# Step 3: Stack inputs and outputs after scaling
inputs_scaled = np.stack([thk_scaled, slopsurfx_scaled, slopsurfy_scaled], axis=-1) # Shape: (time, y, x, 3)
outputs_scaled = np.stack([ubar_scaled, vbar_scaled], axis=-1) # Shape: (time, y, x, 2)
# Check shapes
print(f"Inputs scaled shape: {inputs_scaled.shape}")
print(f"Outputs scaled shape: {outputs_scaled.shape}")
# Visualize the data
time_idx=20
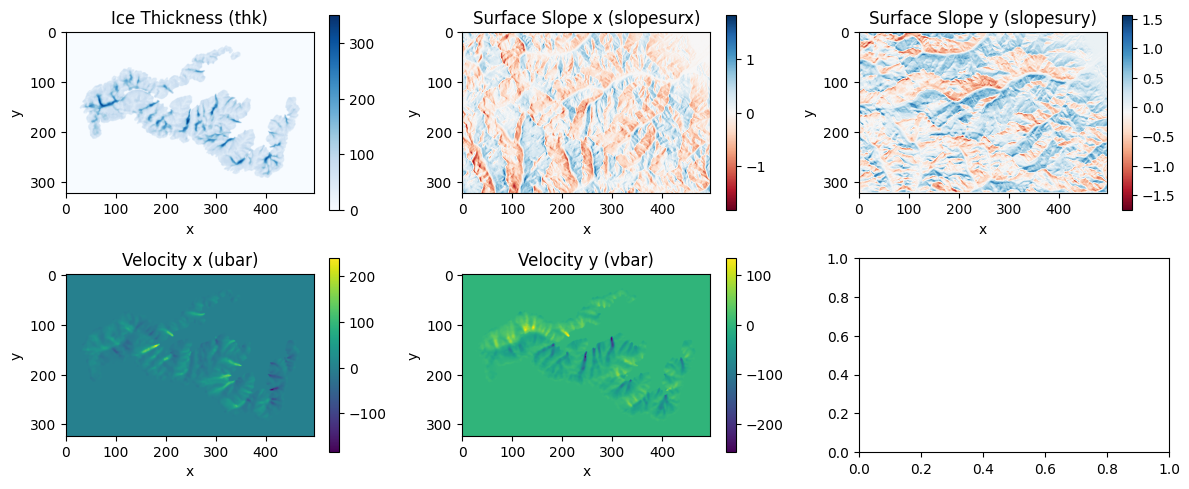
plot_input_output(thk[time_idx], slopsurfx[time_idx], slopsurfy[time_idx], ubar[time_idx], vbar[time_idx])
return inputs_scaled, outputs_scaled, scaling_factors
def augment_data_for_training(inputs_scaled,outputs_scaled):
# Split index for 90-10 split
split_idx = int(0.9 * inputs_scaled.shape[0])
# Train-test split for inputs
X_train = inputs_scaled[:split_idx, :, :, :]
X_test = inputs_scaled[split_idx:, :, :, :]
# Train-test split for outputs
y_train = outputs_scaled[:split_idx, :, :, :]
y_test = outputs_scaled[split_idx:, :, :, :]
# Apply data augmentation
X_train_aug, y_train_aug = augment_data(X_train, y_train)
X_test_aug, y_test_aug = augment_data(X_test,y_test)
# Check shapes
print(f"X_train shape: {X_train_aug.shape}")
print(f"y_train shape: {y_train_aug.shape}")
print(f"X_test shape: {X_test_aug.shape}")
print(f"y_test shape: {y_test_aug.shape}")
return X_test_aug, X_train_aug, y_test_aug, y_train_aug
11.1.2.1.4. Start working on the CNN model#
# Configuration as a dictionary
config = {
"nb_layers": 4, # Number of convolutional layers
"nb_out_filter": 32, # Number of output filters for Conv2D
"conv_ker_size": 3, # Convolution kernel size
"activation": "relu", # Activation function: "relu" or "lrelu"
"dropout_rate": 0.1, # Dropout rate
"regularization": 0.0001 # L2 regularization
}
def build_cnn(nb_inputs, nb_outputs, config):
"""
Build a convolutional neural network (CNN) for glacier velocity field prediction.
Parameters:
- nb_inputs: Number of input channels (thk, slopsurfx, slopsurfy).
- nb_outputs: Number of output channels (ubar, vbar).
- config: Dictionary containing CNN configuration.
Returns:
- A compiled Keras model.
"""
# Define the input layer
inputs = tf.keras.layers.Input(shape=[None, None, nb_inputs])
conv = inputs
# Activation function choice
if config['activation'] == "lrelu":
activation = tf.keras.layers.LeakyReLU(alpha=0.01)
else:
activation = tf.keras.layers.ReLU()
# Stack convolutional layers
for i in range(config['nb_layers']):
conv = tf.keras.layers.Conv2D(
filters=config['nb_out_filter'],
kernel_size=(config['conv_ker_size'], config['conv_ker_size']),
kernel_regularizer=tf.keras.regularizers.l2(config['regularization']),
padding="same"
)(conv)
conv = activation(conv)
conv = tf.keras.layers.Dropout(config['dropout_rate'])(conv)
# Output layer with nb_outputs channels (for ubar, vbar)
outputs = tf.keras.layers.Conv2D(
filters=nb_outputs,
kernel_size=(1, 1),
activation=None
)(conv)
# Return the complete model
model = tf.keras.models.Model(inputs=inputs, outputs=outputs)
return model
# Build and Compile the Model
# Define the number of input channels (thk, slopsurfx, slopsurfy) and output channels (ubar, vbar)
nb_inputs = 3 # thk, slopsurfx, slopsurfy
nb_outputs = 2 # ubar, vbar
# Build the CNN model
model = build_cnn(nb_inputs, nb_outputs, config)
# Compile the model
model.compile(optimizer='adam', loss='mse', metrics=["mae", "mse"])
# Print model summary
model.summary()
Model: "model"
__________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
==================================================================================================
input_1 (InputLayer) [(None, None, None, 0 []
3)]
conv2d (Conv2D) (None, None, None, 896 ['input_1[0][0]']
32)
re_lu (ReLU) (None, None, None, 0 ['conv2d[0][0]',
32) 'conv2d_1[0][0]',
'conv2d_2[0][0]',
'conv2d_3[0][0]']
dropout (Dropout) (None, None, None, 0 ['re_lu[0][0]']
32)
conv2d_1 (Conv2D) (None, None, None, 9248 ['dropout[0][0]']
32)
dropout_1 (Dropout) (None, None, None, 0 ['re_lu[1][0]']
32)
conv2d_2 (Conv2D) (None, None, None, 9248 ['dropout_1[0][0]']
32)
dropout_2 (Dropout) (None, None, None, 0 ['re_lu[2][0]']
32)
conv2d_3 (Conv2D) (None, None, None, 9248 ['dropout_2[0][0]']
32)
dropout_3 (Dropout) (None, None, None, 0 ['re_lu[3][0]']
32)
conv2d_4 (Conv2D) (None, None, None, 66 ['dropout_3[0][0]']
2)
==================================================================================================
Total params: 28,706
Trainable params: 28,706
Non-trainable params: 0
__________________________________________________________________________________________________
2024-10-13 10:08:16.232973: I tensorflow/stream_executor/cuda/cuda_gpu_executor.cc:975] successful NUMA node read from SysFS had negative value (-1), but there must be at least one NUMA node, so returning NUMA node zero
2024-10-13 10:08:16.233305: W tensorflow/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libcudart.so.11.0'; dlerror: libcudart.so.11.0: cannot open shared object file: No such file or directory
2024-10-13 10:08:16.233378: W tensorflow/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libcublas.so.11'; dlerror: libcublas.so.11: cannot open shared object file: No such file or directory
2024-10-13 10:08:16.233409: W tensorflow/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libcublasLt.so.11'; dlerror: libcublasLt.so.11: cannot open shared object file: No such file or directory
2024-10-13 10:08:16.233437: W tensorflow/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libcufft.so.10'; dlerror: libcufft.so.10: cannot open shared object file: No such file or directory
2024-10-13 10:08:16.347368: W tensorflow/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libcusparse.so.11'; dlerror: libcusparse.so.11: cannot open shared object file: No such file or directory
2024-10-13 10:08:16.347428: W tensorflow/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libcudnn.so.8'; dlerror: libcudnn.so.8: cannot open shared object file: No such file or directory
2024-10-13 10:08:16.347433: W tensorflow/core/common_runtime/gpu/gpu_device.cc:1850] Cannot dlopen some GPU libraries. Please make sure the missing libraries mentioned above are installed properly if you would like to use GPU. Follow the guide at https://www.tensorflow.org/install/gpu for how to download and setup the required libraries for your platform.
Skipping registering GPU devices...
2024-10-13 10:08:16.347970: I tensorflow/core/platform/cpu_feature_guard.cc:193] This TensorFlow binary is optimized with oneAPI Deep Neural Network Library (oneDNN) to use the following CPU instructions in performance-critical operations: AVX2 AVX_VNNI FMA
To enable them in other operations, rebuild TensorFlow with the appropriate compiler flags.
# Retrieve the files from the cloud using Pooch.\n",
data_url = 'https://unils-my.sharepoint.com/:u:/g/personal/kejdi_lleshi_unil_ch/EZVN0nazQYFMoFkONuM4788BfSsSe3xjB-jSXYW9JibtHw?download=1'
hash = None
file = pooch.retrieve(data_url, known_hash=hash)
# Load and prepare the necessary dataset
merged_data= load_from_pooch(file)
# Visualize the I/O variables
inputs_scaled, outputs_scaled, scaling_factors = prepare_data(merged_data)
Inputs scaled shape: (101, 323, 497, 3)
Outputs scaled shape: (101, 323, 497, 2)
if train_mode:
# Prepare the data for training
X_test_aug, X_train_aug, y_test_aug, y_train_aug=augment_data_for_training(inputs_scaled,outputs_scaled)
# Train the model
history = model.fit(X_train_aug, y_train_aug, batch_size=8, epochs=100, validation_data=(X_test_aug, y_test_aug))
# Save the trained model to a file
model.save('model.keras')
else :
model_url='https://unils-my.sharepoint.com/:u:/g/personal/kejdi_lleshi_unil_ch/EdNZk6-82ItCmR0oisE135YBTv-TLc7mwPDuU2gPrTojGA?download=1'
hash = None
file = pooch.retrieve(model_url, known_hash=hash)
model = tf.keras.models.load_model(file)
X_train shape: (270, 323, 497, 3)
y_train shape: (270, 323, 497, 2)
X_test shape: (33, 323, 497, 3)
y_test shape: (33, 323, 497, 2)
Epoch 1/100
34/34 [==============================] - 28s 816ms/step - loss: 0.0137 - mae: 0.0315 - mse: 0.0060 - val_loss: 0.0099 - val_mae: 0.0279 - val_mse: 0.0045
Epoch 2/100
34/34 [==============================] - 28s 812ms/step - loss: 0.0093 - mae: 0.0281 - mse: 0.0051 - val_loss: 0.0074 - val_mae: 0.0266 - val_mse: 0.0041
Epoch 3/100
34/34 [==============================] - 28s 833ms/step - loss: 0.0075 - mae: 0.0264 - mse: 0.0047 - val_loss: 0.0061 - val_mae: 0.0231 - val_mse: 0.0036
Epoch 4/100
34/34 [==============================] - 30s 869ms/step - loss: 0.0064 - mae: 0.0236 - mse: 0.0042 - val_loss: 0.0055 - val_mae: 0.0223 - val_mse: 0.0035
Epoch 5/100
34/34 [==============================] - 29s 867ms/step - loss: 0.0059 - mae: 0.0222 - mse: 0.0040 - val_loss: 0.0048 - val_mae: 0.0192 - val_mse: 0.0030
Epoch 6/100
34/34 [==============================] - 29s 863ms/step - loss: 0.0055 - mae: 0.0213 - mse: 0.0038 - val_loss: 0.0045 - val_mae: 0.0184 - val_mse: 0.0029
Epoch 7/100
34/34 [==============================] - 29s 858ms/step - loss: 0.0052 - mae: 0.0206 - mse: 0.0037 - val_loss: 0.0045 - val_mae: 0.0209 - val_mse: 0.0030
Epoch 8/100
34/34 [==============================] - 29s 867ms/step - loss: 0.0050 - mae: 0.0202 - mse: 0.0036 - val_loss: 0.0041 - val_mae: 0.0180 - val_mse: 0.0027
Epoch 9/100
34/34 [==============================] - 29s 853ms/step - loss: 0.0049 - mae: 0.0200 - mse: 0.0035 - val_loss: 0.0040 - val_mae: 0.0174 - val_mse: 0.0026
Epoch 10/100
34/34 [==============================] - 30s 890ms/step - loss: 0.0047 - mae: 0.0199 - mse: 0.0034 - val_loss: 0.0039 - val_mae: 0.0178 - val_mse: 0.0026
Epoch 11/100
34/34 [==============================] - 30s 891ms/step - loss: 0.0048 - mae: 0.0198 - mse: 0.0035 - val_loss: 0.0040 - val_mae: 0.0188 - val_mse: 0.0027
Epoch 12/100
34/34 [==============================] - 30s 887ms/step - loss: 0.0046 - mae: 0.0201 - mse: 0.0034 - val_loss: 0.0037 - val_mae: 0.0168 - val_mse: 0.0025
Epoch 13/100
34/34 [==============================] - 30s 892ms/step - loss: 0.0043 - mae: 0.0188 - mse: 0.0031 - val_loss: 0.0035 - val_mae: 0.0168 - val_mse: 0.0023
Epoch 14/100
34/34 [==============================] - 30s 888ms/step - loss: 0.0043 - mae: 0.0186 - mse: 0.0030 - val_loss: 0.0038 - val_mae: 0.0173 - val_mse: 0.0026
Epoch 15/100
34/34 [==============================] - 30s 889ms/step - loss: 0.0044 - mae: 0.0189 - mse: 0.0032 - val_loss: 0.0039 - val_mae: 0.0205 - val_mse: 0.0027
Epoch 16/100
34/34 [==============================] - 30s 889ms/step - loss: 0.0042 - mae: 0.0185 - mse: 0.0030 - val_loss: 0.0038 - val_mae: 0.0182 - val_mse: 0.0026
Epoch 17/100
34/34 [==============================] - 27s 800ms/step - loss: 0.0043 - mae: 0.0191 - mse: 0.0031 - val_loss: 0.0035 - val_mae: 0.0173 - val_mse: 0.0023
Epoch 18/100
34/34 [==============================] - 25s 731ms/step - loss: 0.0041 - mae: 0.0183 - mse: 0.0029 - val_loss: 0.0036 - val_mae: 0.0184 - val_mse: 0.0024
Epoch 19/100
34/34 [==============================] - 25s 735ms/step - loss: 0.0039 - mae: 0.0178 - mse: 0.0028 - val_loss: 0.0032 - val_mae: 0.0152 - val_mse: 0.0020
Epoch 20/100
34/34 [==============================] - 25s 737ms/step - loss: 0.0041 - mae: 0.0181 - mse: 0.0029 - val_loss: 0.0034 - val_mae: 0.0177 - val_mse: 0.0023
Epoch 21/100
34/34 [==============================] - 25s 723ms/step - loss: 0.0039 - mae: 0.0179 - mse: 0.0027 - val_loss: 0.0034 - val_mae: 0.0164 - val_mse: 0.0022
Epoch 22/100
34/34 [==============================] - 25s 737ms/step - loss: 0.0038 - mae: 0.0173 - mse: 0.0026 - val_loss: 0.0032 - val_mae: 0.0151 - val_mse: 0.0021
Epoch 23/100
34/34 [==============================] - 25s 732ms/step - loss: 0.0038 - mae: 0.0175 - mse: 0.0026 - val_loss: 0.0031 - val_mae: 0.0144 - val_mse: 0.0020
Epoch 24/100
34/34 [==============================] - 25s 735ms/step - loss: 0.0039 - mae: 0.0175 - mse: 0.0027 - val_loss: 0.0032 - val_mae: 0.0155 - val_mse: 0.0020
Epoch 25/100
34/34 [==============================] - 25s 732ms/step - loss: 0.0036 - mae: 0.0164 - mse: 0.0024 - val_loss: 0.0031 - val_mae: 0.0155 - val_mse: 0.0019
Epoch 26/100
34/34 [==============================] - 25s 735ms/step - loss: 0.0036 - mae: 0.0167 - mse: 0.0024 - val_loss: 0.0030 - val_mae: 0.0140 - val_mse: 0.0019
Epoch 27/100
34/34 [==============================] - 25s 726ms/step - loss: 0.0036 - mae: 0.0167 - mse: 0.0025 - val_loss: 0.0029 - val_mae: 0.0143 - val_mse: 0.0018
Epoch 28/100
34/34 [==============================] - 25s 733ms/step - loss: 0.0034 - mae: 0.0158 - mse: 0.0023 - val_loss: 0.0029 - val_mae: 0.0136 - val_mse: 0.0017
Epoch 29/100
34/34 [==============================] - 25s 731ms/step - loss: 0.0036 - mae: 0.0163 - mse: 0.0024 - val_loss: 0.0031 - val_mae: 0.0151 - val_mse: 0.0020
Epoch 30/100
34/34 [==============================] - 25s 743ms/step - loss: 0.0034 - mae: 0.0160 - mse: 0.0023 - val_loss: 0.0029 - val_mae: 0.0149 - val_mse: 0.0018
Epoch 31/100
34/34 [==============================] - 25s 726ms/step - loss: 0.0035 - mae: 0.0161 - mse: 0.0024 - val_loss: 0.0028 - val_mae: 0.0134 - val_mse: 0.0017
Epoch 32/100
34/34 [==============================] - 25s 727ms/step - loss: 0.0033 - mae: 0.0153 - mse: 0.0021 - val_loss: 0.0028 - val_mae: 0.0136 - val_mse: 0.0016
Epoch 33/100
34/34 [==============================] - 25s 733ms/step - loss: 0.0032 - mae: 0.0151 - mse: 0.0021 - val_loss: 0.0028 - val_mae: 0.0134 - val_mse: 0.0017
Epoch 34/100
34/34 [==============================] - 25s 735ms/step - loss: 0.0032 - mae: 0.0151 - mse: 0.0021 - val_loss: 0.0026 - val_mae: 0.0141 - val_mse: 0.0015
Epoch 35/100
34/34 [==============================] - 25s 731ms/step - loss: 0.0032 - mae: 0.0151 - mse: 0.0021 - val_loss: 0.0028 - val_mae: 0.0135 - val_mse: 0.0017
Epoch 36/100
34/34 [==============================] - 25s 734ms/step - loss: 0.0032 - mae: 0.0149 - mse: 0.0020 - val_loss: 0.0027 - val_mae: 0.0140 - val_mse: 0.0016
Epoch 37/100
34/34 [==============================] - 25s 732ms/step - loss: 0.0032 - mae: 0.0150 - mse: 0.0020 - val_loss: 0.0026 - val_mae: 0.0133 - val_mse: 0.0015
Epoch 38/100
34/34 [==============================] - 25s 738ms/step - loss: 0.0033 - mae: 0.0157 - mse: 0.0022 - val_loss: 0.0029 - val_mae: 0.0134 - val_mse: 0.0018
Epoch 39/100
34/34 [==============================] - 25s 738ms/step - loss: 0.0031 - mae: 0.0149 - mse: 0.0020 - val_loss: 0.0025 - val_mae: 0.0125 - val_mse: 0.0014
Epoch 40/100
34/34 [==============================] - 25s 737ms/step - loss: 0.0031 - mae: 0.0145 - mse: 0.0020 - val_loss: 0.0026 - val_mae: 0.0138 - val_mse: 0.0015
Epoch 41/100
34/34 [==============================] - 27s 790ms/step - loss: 0.0030 - mae: 0.0145 - mse: 0.0019 - val_loss: 0.0025 - val_mae: 0.0122 - val_mse: 0.0014
Epoch 42/100
34/34 [==============================] - 30s 897ms/step - loss: 0.0030 - mae: 0.0144 - mse: 0.0019 - val_loss: 0.0027 - val_mae: 0.0139 - val_mse: 0.0016
Epoch 43/100
34/34 [==============================] - 29s 851ms/step - loss: 0.0032 - mae: 0.0152 - mse: 0.0021 - val_loss: 0.0030 - val_mae: 0.0139 - val_mse: 0.0019
Epoch 44/100
34/34 [==============================] - 29s 839ms/step - loss: 0.0030 - mae: 0.0145 - mse: 0.0019 - val_loss: 0.0025 - val_mae: 0.0128 - val_mse: 0.0014
Epoch 45/100
34/34 [==============================] - 29s 841ms/step - loss: 0.0030 - mae: 0.0144 - mse: 0.0019 - val_loss: 0.0025 - val_mae: 0.0126 - val_mse: 0.0014
Epoch 46/100
34/34 [==============================] - 29s 846ms/step - loss: 0.0029 - mae: 0.0141 - mse: 0.0018 - val_loss: 0.0025 - val_mae: 0.0118 - val_mse: 0.0014
Epoch 47/100
34/34 [==============================] - 28s 839ms/step - loss: 0.0028 - mae: 0.0138 - mse: 0.0018 - val_loss: 0.0024 - val_mae: 0.0115 - val_mse: 0.0013
Epoch 48/100
34/34 [==============================] - 29s 849ms/step - loss: 0.0028 - mae: 0.0138 - mse: 0.0017 - val_loss: 0.0024 - val_mae: 0.0116 - val_mse: 0.0013
Epoch 49/100
34/34 [==============================] - 29s 857ms/step - loss: 0.0028 - mae: 0.0138 - mse: 0.0018 - val_loss: 0.0024 - val_mae: 0.0118 - val_mse: 0.0013
Epoch 50/100
34/34 [==============================] - 32s 957ms/step - loss: 0.0028 - mae: 0.0137 - mse: 0.0017 - val_loss: 0.0025 - val_mae: 0.0128 - val_mse: 0.0014
Epoch 51/100
34/34 [==============================] - 30s 888ms/step - loss: 0.0028 - mae: 0.0137 - mse: 0.0017 - val_loss: 0.0024 - val_mae: 0.0124 - val_mse: 0.0013
Epoch 52/100
34/34 [==============================] - 29s 853ms/step - loss: 0.0030 - mae: 0.0149 - mse: 0.0020 - val_loss: 0.0024 - val_mae: 0.0122 - val_mse: 0.0013
Epoch 53/100
34/34 [==============================] - 29s 848ms/step - loss: 0.0029 - mae: 0.0141 - mse: 0.0018 - val_loss: 0.0025 - val_mae: 0.0119 - val_mse: 0.0014
Epoch 54/100
34/34 [==============================] - 29s 853ms/step - loss: 0.0029 - mae: 0.0139 - mse: 0.0018 - val_loss: 0.0023 - val_mae: 0.0115 - val_mse: 0.0013
Epoch 55/100
34/34 [==============================] - 29s 855ms/step - loss: 0.0029 - mae: 0.0141 - mse: 0.0018 - val_loss: 0.0025 - val_mae: 0.0124 - val_mse: 0.0014
Epoch 56/100
34/34 [==============================] - 29s 856ms/step - loss: 0.0028 - mae: 0.0137 - mse: 0.0017 - val_loss: 0.0023 - val_mae: 0.0117 - val_mse: 0.0012
Epoch 57/100
34/34 [==============================] - 29s 853ms/step - loss: 0.0027 - mae: 0.0130 - mse: 0.0016 - val_loss: 0.0022 - val_mae: 0.0115 - val_mse: 0.0012
Epoch 58/100
34/34 [==============================] - 29s 854ms/step - loss: 0.0028 - mae: 0.0140 - mse: 0.0017 - val_loss: 0.0024 - val_mae: 0.0119 - val_mse: 0.0013
Epoch 59/100
34/34 [==============================] - 28s 823ms/step - loss: 0.0027 - mae: 0.0133 - mse: 0.0016 - val_loss: 0.0023 - val_mae: 0.0108 - val_mse: 0.0012
Epoch 60/100
34/34 [==============================] - 25s 722ms/step - loss: 0.0026 - mae: 0.0129 - mse: 0.0016 - val_loss: 0.0022 - val_mae: 0.0115 - val_mse: 0.0011
Epoch 61/100
34/34 [==============================] - 25s 740ms/step - loss: 0.0026 - mae: 0.0129 - mse: 0.0016 - val_loss: 0.0023 - val_mae: 0.0113 - val_mse: 0.0012
Epoch 62/100
34/34 [==============================] - 25s 731ms/step - loss: 0.0027 - mae: 0.0131 - mse: 0.0016 - val_loss: 0.0022 - val_mae: 0.0116 - val_mse: 0.0012
Epoch 63/100
34/34 [==============================] - 25s 727ms/step - loss: 0.0027 - mae: 0.0134 - mse: 0.0017 - val_loss: 0.0024 - val_mae: 0.0133 - val_mse: 0.0014
Epoch 64/100
34/34 [==============================] - 25s 723ms/step - loss: 0.0027 - mae: 0.0133 - mse: 0.0016 - val_loss: 0.0023 - val_mae: 0.0114 - val_mse: 0.0013
Epoch 65/100
34/34 [==============================] - 25s 733ms/step - loss: 0.0028 - mae: 0.0143 - mse: 0.0018 - val_loss: 0.0024 - val_mae: 0.0135 - val_mse: 0.0013
Epoch 66/100
34/34 [==============================] - 25s 726ms/step - loss: 0.0028 - mae: 0.0145 - mse: 0.0018 - val_loss: 0.0023 - val_mae: 0.0118 - val_mse: 0.0012
Epoch 67/100
34/34 [==============================] - 25s 735ms/step - loss: 0.0028 - mae: 0.0141 - mse: 0.0018 - val_loss: 0.0025 - val_mae: 0.0143 - val_mse: 0.0015
Epoch 68/100
34/34 [==============================] - 25s 735ms/step - loss: 0.0029 - mae: 0.0144 - mse: 0.0018 - val_loss: 0.0024 - val_mae: 0.0135 - val_mse: 0.0014
Epoch 69/100
34/34 [==============================] - 25s 731ms/step - loss: 0.0026 - mae: 0.0129 - mse: 0.0016 - val_loss: 0.0024 - val_mae: 0.0126 - val_mse: 0.0014
Epoch 70/100
34/34 [==============================] - 25s 732ms/step - loss: 0.0027 - mae: 0.0136 - mse: 0.0017 - val_loss: 0.0023 - val_mae: 0.0113 - val_mse: 0.0012
Epoch 71/100
34/34 [==============================] - 25s 722ms/step - loss: 0.0026 - mae: 0.0128 - mse: 0.0015 - val_loss: 0.0021 - val_mae: 0.0107 - val_mse: 0.0011
Epoch 72/100
34/34 [==============================] - 25s 724ms/step - loss: 0.0026 - mae: 0.0126 - mse: 0.0015 - val_loss: 0.0021 - val_mae: 0.0109 - val_mse: 0.0011
Epoch 73/100
34/34 [==============================] - 24s 717ms/step - loss: 0.0026 - mae: 0.0127 - mse: 0.0015 - val_loss: 0.0021 - val_mae: 0.0104 - val_mse: 0.0011
Epoch 74/100
34/34 [==============================] - 24s 721ms/step - loss: 0.0028 - mae: 0.0142 - mse: 0.0018 - val_loss: 0.0024 - val_mae: 0.0122 - val_mse: 0.0013
Epoch 75/100
34/34 [==============================] - 24s 719ms/step - loss: 0.0027 - mae: 0.0139 - mse: 0.0017 - val_loss: 0.0022 - val_mae: 0.0111 - val_mse: 0.0012
Epoch 76/100
34/34 [==============================] - 25s 724ms/step - loss: 0.0025 - mae: 0.0126 - mse: 0.0015 - val_loss: 0.0021 - val_mae: 0.0111 - val_mse: 0.0011
Epoch 77/100
34/34 [==============================] - 25s 728ms/step - loss: 0.0025 - mae: 0.0126 - mse: 0.0015 - val_loss: 0.0021 - val_mae: 0.0108 - val_mse: 0.0011
Epoch 78/100
34/34 [==============================] - 24s 719ms/step - loss: 0.0025 - mae: 0.0126 - mse: 0.0015 - val_loss: 0.0022 - val_mae: 0.0119 - val_mse: 0.0012
Epoch 79/100
34/34 [==============================] - 25s 734ms/step - loss: 0.0026 - mae: 0.0130 - mse: 0.0015 - val_loss: 0.0021 - val_mae: 0.0106 - val_mse: 0.0011
Epoch 80/100
34/34 [==============================] - 25s 722ms/step - loss: 0.0024 - mae: 0.0123 - mse: 0.0014 - val_loss: 0.0021 - val_mae: 0.0100 - val_mse: 0.0010
Epoch 81/100
34/34 [==============================] - 25s 723ms/step - loss: 0.0025 - mae: 0.0124 - mse: 0.0015 - val_loss: 0.0020 - val_mae: 0.0105 - val_mse: 9.8833e-04
Epoch 82/100
34/34 [==============================] - 25s 722ms/step - loss: 0.0025 - mae: 0.0125 - mse: 0.0015 - val_loss: 0.0023 - val_mae: 0.0133 - val_mse: 0.0013
Epoch 83/100
34/34 [==============================] - 25s 720ms/step - loss: 0.0025 - mae: 0.0128 - mse: 0.0015 - val_loss: 0.0021 - val_mae: 0.0105 - val_mse: 0.0011
Epoch 84/100
34/34 [==============================] - 25s 725ms/step - loss: 0.0025 - mae: 0.0125 - mse: 0.0015 - val_loss: 0.0020 - val_mae: 0.0106 - val_mse: 9.8987e-04
Epoch 85/100
34/34 [==============================] - 24s 721ms/step - loss: 0.0025 - mae: 0.0125 - mse: 0.0014 - val_loss: 0.0021 - val_mae: 0.0119 - val_mse: 0.0011
Epoch 86/100
34/34 [==============================] - 25s 724ms/step - loss: 0.0025 - mae: 0.0127 - mse: 0.0015 - val_loss: 0.0022 - val_mae: 0.0125 - val_mse: 0.0012
Epoch 87/100
34/34 [==============================] - 25s 725ms/step - loss: 0.0026 - mae: 0.0134 - mse: 0.0016 - val_loss: 0.0020 - val_mae: 0.0108 - val_mse: 0.0010
Epoch 88/100
34/34 [==============================] - 24s 716ms/step - loss: 0.0025 - mae: 0.0125 - mse: 0.0015 - val_loss: 0.0020 - val_mae: 0.0101 - val_mse: 0.0010
Epoch 89/100
34/34 [==============================] - 25s 734ms/step - loss: 0.0024 - mae: 0.0122 - mse: 0.0014 - val_loss: 0.0020 - val_mae: 0.0101 - val_mse: 9.8987e-04
Epoch 90/100
34/34 [==============================] - 24s 722ms/step - loss: 0.0024 - mae: 0.0122 - mse: 0.0014 - val_loss: 0.0021 - val_mae: 0.0103 - val_mse: 0.0011
Epoch 91/100
34/34 [==============================] - 25s 730ms/step - loss: 0.0024 - mae: 0.0122 - mse: 0.0014 - val_loss: 0.0021 - val_mae: 0.0107 - val_mse: 0.0011
Epoch 92/100
34/34 [==============================] - 25s 732ms/step - loss: 0.0024 - mae: 0.0122 - mse: 0.0014 - val_loss: 0.0020 - val_mae: 0.0104 - val_mse: 0.0010
Epoch 93/100
34/34 [==============================] - 25s 729ms/step - loss: 0.0024 - mae: 0.0121 - mse: 0.0014 - val_loss: 0.0020 - val_mae: 0.0097 - val_mse: 9.7307e-04
Epoch 94/100
34/34 [==============================] - 25s 723ms/step - loss: 0.0024 - mae: 0.0119 - mse: 0.0014 - val_loss: 0.0019 - val_mae: 0.0098 - val_mse: 9.3450e-04
Epoch 95/100
34/34 [==============================] - 25s 726ms/step - loss: 0.0024 - mae: 0.0121 - mse: 0.0014 - val_loss: 0.0020 - val_mae: 0.0104 - val_mse: 9.6628e-04
Epoch 96/100
34/34 [==============================] - 25s 722ms/step - loss: 0.0027 - mae: 0.0137 - mse: 0.0017 - val_loss: 0.0021 - val_mae: 0.0118 - val_mse: 0.0011
Epoch 97/100
34/34 [==============================] - 25s 726ms/step - loss: 0.0024 - mae: 0.0121 - mse: 0.0014 - val_loss: 0.0019 - val_mae: 0.0096 - val_mse: 9.5879e-04
Epoch 98/100
34/34 [==============================] - 24s 719ms/step - loss: 0.0023 - mae: 0.0120 - mse: 0.0014 - val_loss: 0.0020 - val_mae: 0.0104 - val_mse: 0.0010
Epoch 99/100
34/34 [==============================] - 25s 728ms/step - loss: 0.0027 - mae: 0.0138 - mse: 0.0017 - val_loss: 0.0022 - val_mae: 0.0126 - val_mse: 0.0012
Epoch 100/100
34/34 [==============================] - 25s 731ms/step - loss: 0.0024 - mae: 0.0119 - mse: 0.0013 - val_loss: 0.0020 - val_mae: 0.0106 - val_mse: 0.0010
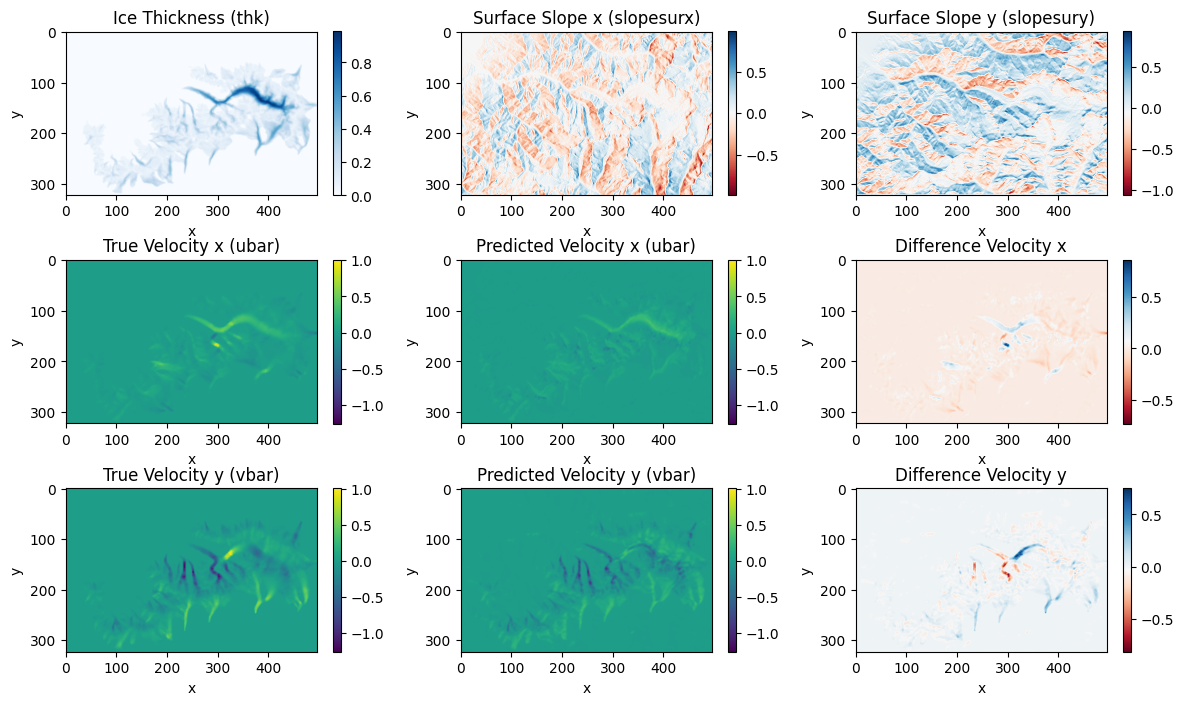
# Visualise the performance of the trained model by making predictions
predicted_outputs = model.predict(X_test_aug)
# Separate predicted outputs into ubar and vbar components
pred_ubar = predicted_outputs[..., 0] # First channel is ubar
pred_vbar = predicted_outputs[..., 1] # Second channel is vbar
# Call the plot function for a specific time index, e.g., 0
time_idx = 2
plot_comparison(X_test_aug[..., 0], X_test_aug[..., 1], X_test_aug[..., 2], y_test_aug[..., 0], y_test_aug[..., 1], pred_ubar, pred_vbar, time_idx)
2/2 [==============================] - 1s 22ms/step
#Plot the Learning curve
if train_mode:
plt.figure(figsize=(10, 6))
# Plot training loss
plt.plot(history.history['loss'], label='Training Loss')
# Plot validation loss
plt.plot(history.history['val_loss'], label='Validation Loss')
# Add labels and legend
plt.title('Learning Curve (Loss vs. Epochs)')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend(loc='upper right')
plt.savefig("Lr.png")
# Show plot
plt.show()
11.1.2.2. Implementatiing the hybrid model#
For the hybrid model, we will implement the mass conservation equation in a numerical shceme. The main difference with the first approach will be how we calculate u(x,y). The emulator we trained above, we plug it in the mass conservation equation to calculate the flux.
Now we will need a couple of helper functions, compute_divflux() and compute_gradient_tf(), for each itteration of the numerical scheme.
Remember that the velocity field is mainly dependent on the slope and the thckness of the glacier.
11.1.2.2.1. Helping functions for the hybrid model#
@tf.function()
def compute_divflux(u, v, h, dx, dy):
"""
Upwind computation of the divergence of the flux: d(u h)/dx + d(v h)/dy
Parameters:
- u: x-component of velocity (2D tensor).
- v: y-component of velocity (2D tensor).
- h: ice thickness (2D tensor).
- dx: grid spacing in the x-direction (float).
- dy: grid spacing in the y-direction (float).
Returns:
- divflux: divergence of flux (2D tensor).
"""
# Compute u and v on the staggered grid
u = tf.concat([u[:, 0:1], 0.5 * (u[:, :-1] + u[:, 1:]), u[:, -1:]], 1) # shape (ny, nx+1)
v = tf.concat([v[0:1, :], 0.5 * (v[:-1, :] + v[1:, :]), v[-1:, :]], 0) # shape (ny+1, nx)
# Extend h with constant value at the domain boundaries
Hx = tf.pad(h, [[0, 0], [1, 1]], "CONSTANT") # shape (ny, nx+2)
Hy = tf.pad(h, [[1, 1], [0, 0]], "CONSTANT") # shape (ny+2, nx)
# Compute fluxes by selecting the upwind quantities
Qx = u * tf.where(u > 0, Hx[:, :-1], Hx[:, 1:]) # shape (ny, nx+1)
Qy = v * tf.where(v > 0, Hy[:-1, :], Hy[1:, :]) # shape (ny+1, nx)
# Compute the divergence, final shape is (ny, nx)
divflux = (Qx[:, 1:] - Qx[:, :-1]) / dx + (Qy[1:, :] - Qy[:-1, :]) / dy
return divflux
@tf.function()
def compute_gradient_tf(s, dx, dy):
"""
Compute spatial 2D gradient of a given field.
Parameters:
- s: surface elevation (2D tensor).
- dx: grid spacing in the x-direction (float).
- dy: grid spacing in the y-direction (float).
Returns:
- diffx: gradient in the x-direction (2D tensor).
- diffy: gradient in the y-direction (2D tensor).
"""
EX = tf.concat([1.5 * s[:, 0:1] - 0.5 * s[:, 1:2], 0.5 * s[:, :-1] + 0.5 * s[:, 1:], 1.5 * s[:, -1:] - 0.5 * s[:, -2:-1]], 1)
diffx = (EX[:, 1:] - EX[:, :-1]) / dx
EY = tf.concat([1.5 * s[0:1, :] - 0.5 * s[1:2, :], 0.5 * s[:-1, :] + 0.5 * s[1:, :], 1.5 * s[-1:, :] - 0.5 * s[-2:-1, :]], 0)
diffy = (EY[1:, :] - EY[:-1, :]) / dy
return diffx, diffy
def apply_boundary_condition(H_ice, boundary_width=5):
"""
Apply boundary condition to the ice thickness field `H_ice`.
The ice thickness will linearly decrease to zero starting from `boundary_width` pixels away from the boundary.
Parameters:
- H_ice: 2D numpy array representing ice thickness.
- boundary_width: Number of pixels from the boundary where H_ice starts to decrease.
Returns:
- Modified H_ice with boundary condition applied.
"""
ny, nx = H_ice.shape # Get the dimensions of the ice thickness field
# Create linear ramps
ramp = np.linspace(1, 0, boundary_width) # Ramp that linearly decreases from 1 to 0
# Apply boundary condition to the left boundary
H_ice[:, :boundary_width] *= ramp[::-1] # Decrease from boundary to 5 pixels inwards
# Apply boundary condition to the right boundary
H_ice[:, -boundary_width:] *= ramp # Decrease from 5 pixels inwards to the boundary
# Apply boundary condition to the top boundary
H_ice[:boundary_width, :] *= ramp[::-1, np.newaxis] # Decrease vertically from top boundary
# Apply boundary condition to the bottom boundary
H_ice[-boundary_width:, :] *= ramp[:, np.newaxis] # Decrease vertically to bottom boundary
return H_ice
11.1.2.2.2. Run the hybrid model#
# Physical parameters
Lx = 49700 # Domain length in x (m)
Ly = 32300 # Domain length in y (m)
ttot = 700 # Time limit (yr)
grad_b = 0.001 # Mass balance gradient (no unit)
b_max = 0.5 # Maximum precip (m/yr)
Z_ELA = 3000 # Elevation of equilibrium line altitude (m)
# Initialization & load data
nout = 50 # Frequency of plotting
dtmax = 1 # maximum time step
cfl = 0.20
dx = 100
dy = 100 # Cell size in y
nx=int(Lx/dx)
ny=int(Ly/dy)
x = np.linspace(0, Lx, nx) # x-coordinates
y = np.linspace(0, Ly, ny) # y-coordinates
H_ice = np.zeros((ny, nx)) # Initial ice thickness
Z_surf = Z_topo + H_ice # Initial ice surface
# Compute gradients of surface elevation (slopes)
slopsurfx, slopsurfy = compute_gradient_tf(Z_surf, dx, dx)
time = tf.cast(0.0, tf.float32) # Initial time as float32
dt = tf.cast(dtmax, tf.float32) # Cast dtmax to float32e
it = 0
# Ensure all arrays are float32
H_ice = tf.cast(H_ice, tf.float32)
slopsurfx = tf.cast(slopsurfx, tf.float32)
slopsurfy = tf.cast(slopsurfy, tf.float32)
Z_surf = tf.cast(Z_surf, tf.float32)
Z_topo = tf.cast(Z_topo, tf.float32)
#Fields need to be scaled
# Loop
while time < ttot:
# Update time
time += dt
it += 1
# Calculate H_avg, size (ny-1, nx-1)
H_avg = 0.25 * (H_ice[:-1, :-1] + H_ice[1:, 1:] + H_ice[:-1, 1:] + H_ice[1:, :-1])
# Scale the inputs with stored scaling factors
H_ice_scaled = H_ice / scaling_factors["thk"]
slopsurfx_scaled = slopsurfx / scaling_factors["slopsurfx"]
slopsurfy_scaled = slopsurfy / scaling_factors["slopsurfy"]
# Combine scaled inputs
input_data_scaled = np.stack([H_ice_scaled, slopsurfx_scaled, slopsurfy_scaled], axis=-1)
input_data_scaled = np.expand_dims(input_data_scaled, axis=0) # Add batch dimension
# Step 2: Use the trained model to predict ubar (x-velocity) and vbar (y-velocity)
ubar_vbar_pred = model.predict(input_data_scaled, verbose=0)
ubar = ubar_vbar_pred[0, :, :, 0] * scaling_factors["ubar"] # x-component of velocity (ubar)
vbar = ubar_vbar_pred[0, :, :, 1] * scaling_factors["vbar"] # y-component of velocity (vbar)
# Step 3: Compute maximum velocity for CFL condition
vel_max = max(
tf.math.reduce_max(tf.math.abs(ubar)),
tf.math.reduce_max(tf.math.abs(vbar)),
).numpy()
# Step 4: Compute time step (CFL condition)
dt = tf.cast(tf.minimum(cfl * dx / vel_max, dtmax), tf.float32)
# Step 5: Update rule (diffusion): Compute the change in thickness (dH/dt)
dHdt = -compute_divflux(ubar, vbar, H_ice, dx, dx)
# Update ice thickness (ensure no negative values)
H_ice += dt * dHdt
# Define the SMB (Surface Mass Balance)
b = tf.minimum(grad_b * (Z_surf - Z_ELA), b_max)
# Update rule (mass balance)
H_ice += dt * b
# Update rule (positive thickness)
H_ice = np.maximum(H_ice, 0)
# Apply the boundary condition before the next iteration
H_ice = apply_boundary_condition(H_ice)
# Update surface topography
Z_surf = Z_topo + H_ice
# Compute gradients of surface elevation (slopes)
slopsurfx, slopsurfy = compute_gradient_tf(Z_surf, dx, dx)
# Update ELA after 500 years
if time > 500:
Z_ELA = 2700
# Display
if it % nout == 0:
clear_output(wait=True) # Clear the previous output in the notebook
plt.figure(2, figsize=(11, 4), dpi=200)
# First subplot: Ice surface
plt.subplot(1, 2, 1)
plt.imshow(Z_surf, extent=[0, Lx/1000, 0, Ly/1000], cmap='terrain', origin='lower')
plt.colorbar(label='Elevation (m)')
plt.title('Ice Surface at ' + str(int(time)) + ' y')
plt.xlabel('Distance, km')
plt.ylabel('Distance, km')
# Second subplot: Ice thickness
plt.subplot(1, 2, 2)
plt.imshow(np.where(H_ice > 0, H_ice, np.nan), extent=[0, Lx/1000, 0, Ly/1000], cmap='jet', origin='lower')
plt.colorbar(label='Ice Thickness (m)')
plt.title('Ice Thickness at ' + str(int(time)) + ' y')
plt.xlabel('Distance, km')
plt.ylabel('Distance, km')
# Show the plot
plt.show()
Q: What are some dissadvantage of the hybrid models?
Border conditions are difficoult to implement.
The model is as good as our data is
Q: What are some other fields where we can use Hybrid Models?
1
2