8.1. (Exercise) Graph Neural Networks with PyTorch

Figure: An AI artwork on GNN and weather forcasting created by GPT4, 2024

In the beginning, this notebook was designed to be run on Google Colab and we highly recommend clicking on the Google Colab badge to proceed. Aiming at covering the knowledge of Labonne’s Chapters 01 + 02, this jupyter notebook builds on the related colab assignments in CS224W: Machine Learning with Graphs, originally offered by Prof. Jure and his team Stanford University.

As you see in the previous image, we hope you are inspired to get familiar with the basic concepts of graph mining and Graph Neural Networks through this notebook. All of them are mainly implemented through two libraries, NetworkX and PyTorch Geometric. In this notebook, we will write a full pipeline for learning Node Embeddings and introducing the Graph Neural Networks. We will go through the following 4 steps.

To start, we will load a classic graph in network science, the Karate Club Network. Then we will offer the basic tutorial for NetworkX and then explore multiple graph statistics.

With the help of PyTorch Geometric tutorial, we will then work together to transform the graph structure into a PyTorch tensor, so that we can perform machine learning over the graph.

And we will finish the first learning algorithm on graphs: a node embedding model. For simplicity, our model here is simpler than classical algorithms applied in the research, such as DeepWalk or node2vec. But it’s still rewarding and challenging, as we will write it from scratch via PyTorch.

Finally, you can implement one of the most simple GNN operators, the Graph Convolutional Networks (Kipf et al. (2017)). We hope you can use this 3-layers GCN to learn embeddings that will be useful to classify each node into its community among the Karate Club Network.

8.2. Graph Basics

To start, we will load a classic graph in network science, the Karate Club Network. We will explore multiple graph statistics for that graph.

8.2.1. NetworkX Tutorial

NetworkX is one of the most frequently used Python packages to create, manipulate, and mine graphs.

Main parts of this tutorial are adapted from https://colab.research.google.com/github/jdwittenauer/ipython-notebooks/blob/master/notebooks/libraries/NetworkX.ipynb#scrollTo=zA1OO6huHeV6

You can explore more NetworkX functions through its documentation.

8.2.1.1. Setup

# Upgrade packages
!pip install --upgrade scipy networkx

Requirement already satisfied: scipy in c:\users\tbeucler\.conda\envs\jb\lib\site-packages (1.13.1)
Requirement already satisfied: networkx in c:\users\tbeucler\.conda\envs\jb\lib\site-packages (3.2.1)
Requirement already satisfied: numpy<2.3,>=1.22.4 in c:\users\tbeucler\.conda\envs\jb\lib\site-packages (from scipy) (1.25.1)

# Import the NetworkX package
import networkx as nx

8.2.1.2. Graph

NetworkX provides several classes to store different types of graphs, such as directed and undirected graph. It also provides classes to create multigraphs (both directed and undirected).

# Create an undirected graph G
G = nx.Graph()
print(G.is_directed())

# Create a directed graph H
H = nx.DiGraph()
print(H.is_directed())

# Add graph level attribute
G.graph["Name"] = "Bar"
print(G.graph)

False
True
{'Name': 'Bar'}

8.2.1.3. Node

Nodes (with attributes) can be easily added to NetworkX graphs.

# Add one node with node level attributes
G.add_node(0, feature=5, label=0)

# Get attributes of the node 0
node_0_attr = G.nodes[0]
print("Node 0 has the attributes {}".format(node_0_attr))

Node 0 has the attributes {'feature': 5, 'label': 0}

G.nodes(data=True)

NodeDataView({0: {'feature': 5, 'label': 0}})

# Add multiple nodes with attributes
G.add_nodes_from([
  (1, {"feature": 1, "label": 1}),
  (2, {"feature": 2, "label": 2})
]) #(node, attrdict)

# Loop through all the nodes
# Set data=True will return node attributes
for node in G.nodes(data=True):
  print(node)

# Get number of nodes
num_nodes = G.number_of_nodes()
print("G has {} nodes".format(num_nodes))

(0, {'feature': 5, 'label': 0})
(1, {'feature': 1, 'label': 1})
(2, {'feature': 2, 'label': 2})
G has 3 nodes

8.2.1.4. Edge

Similar to nodes, edges (with attributes) can also be easily added to NetworkX graphs.

# Add one edge with edge weight 0.5
G.add_edge(0, 1, weight=0.5)

# Get attributes of the edge (0, 1)
edge_0_1_attr = G.edges[(0, 1)]
print("Edge (0, 1) has the attributes {}".format(edge_0_1_attr))

Edge (0, 1) has the attributes {'weight': 0.5}

# Add multiple edges with edge weights
G.add_edges_from([
  (1, 2, {"weight": 0.3}),
  (2, 0, {"weight": 0.1})
])

# Loop through all the edges
# Here there is no data=True, so only the edge will be returned
for edge in G.edges():
  print(edge)

# Get number of edges
num_edges = G.number_of_edges()
print("G has {} edges".format(num_edges))

(0, 1)
(0, 2)
(1, 2)
G has 3 edges

8.2.1.5. Graph Visualization

NetworkX also provides tooling to conventiently visualize graphs.

# Draw the graph
nx.draw(G, with_labels = True)

8.2.1.6. Node Degree and Neighbor

node_id = 1

# Degree of node 1
print("Node {} has degree {}".format(node_id, G.degree[node_id]))

# Get neighbor of node 1
for neighbor in G.neighbors(node_id):
  print("Node {} has neighbor {}".format(node_id, neighbor))

Node 1 has degree 2
Node 1 has neighbor 0
Node 1 has neighbor 2

8.2.1.7. Other Functionalities

NetworkX also provides plenty of useful methods to study graphs. Here is an example to get PageRank of nodes.

num_nodes = 4

# Create a new path like graph and change it to a directed graph
G = nx.DiGraph(nx.path_graph(num_nodes))
nx.draw(G, with_labels = True)

# Get the PageRank
pr = nx.pagerank(G, alpha=0.8)
pr

{0: 0.17857162031103999,
 1: 0.32142837968896,
 2: 0.32142837968896,
 3: 0.17857162031103999}

8.2.2. Exercise

8.2.2.1. Zachary’s karate club network

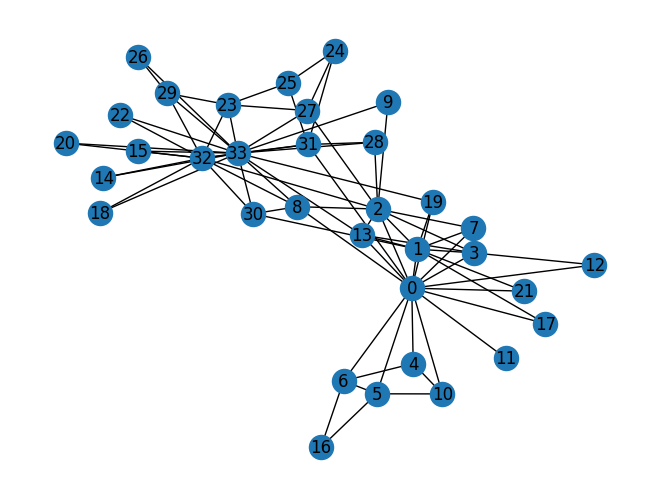
The Karate Club Network is a graph which describes a social network of 34 members of a karate club and documents links between members who interacted outside the club.

# Find the karate club network from the NetworkX
G_karate = nx.karate_club_graph()

# G is an undirected graph
type(G_karate)

# Visualize the graph
nx.draw(G_karate, with_labels = True)

8.2.2.2. Question 1: What is the average degree of the karate club network?

def average_degree(num_edges, num_nodes):
  # TODO: Implement this function that takes number of edges
  # and number of nodes, and returns the average node degree of
  # the graph. Round the result to nearest integer (for example
  # 3.3 will be rounded to 3 and 3.7 will be rounded to 4)

  avg_degree = 0

  ############# Your code here ############
  #########################################

  return avg_degree

num_edges = G_karate.number_of_edges()
num_nodes = G_karate.number_of_nodes()
avg_degree = average_degree(num_edges, num_nodes)
print("Average degree of karate club network is {}".format(avg_degree))

Average degree of karate club network is 0

8.2.2.3. Question 2: What is the average clustering coefficient of the karate club network?

def average_clustering_coefficient(G_karate):
  # TODO: Implement this function that takes a nx.Graph
  # and returns the average clustering coefficient. Round
  # the result to 2 decimal places (for example 3.333 will
  # be rounded to 3.33 and 3.7571 will be rounded to 3.76)

  avg_cluster_coef = 0

  ############# Your code here ############
  ## Note:
  ## 1: Please use the appropriate NetworkX clustering function
  #########################################

  return avg_cluster_coef

avg_cluster_coef = average_clustering_coefficient(G_karate)
print("Average clustering coefficient of karate club network is {}".format(avg_cluster_coef))

Average clustering coefficient of karate club network is 0

8.2.2.4. Question 3: What is the PageRank value for node 0 (node with id 0) after one PageRank iteration?

Page Rank measures importance of nodes in a graph using the link structure of the web. A “vote” from an important page is worth more. Specifically, if a page \(i\) with importance \(r_i\) has \(d_i\) out-links, then each link gets \(\frac{r_i}{d_i}\) votes. Thus, the importance of a Page \(j\), represented as \(r_j\) is the sum of the votes on its in links. $\(r_j = \sum_{i \rightarrow j} \frac{r_i}{d_i}\)\( , where \)d_i\( is the out degree of node \)i$.

The PageRank algorithm (used by Google) outputs a probability distribution which represent the likelihood of a random surfer clicking on links will arrive at any particular page. At each time step, the random surfer has two options

• With prob. \(\beta\), follow a link at random

• With prob. \(1- \beta\), jump to a random page

Thus, the importance of a particular page is calculated with the following PageRank equation: $\(r_j = \sum_{i \rightarrow j} \beta \frac{r_i}{d_i} + (1 - \beta) \frac{1}{N}\)$

Please complete the code block by implementing the above PageRank equation for node 0.

Note: You can refer to more information from the Stanford’s slides

def one_iter_pagerank(G_karate, beta, r0, node_id):
  # TODO: Implement this function that takes a nx.Graph, beta, r0 and node id.
  # The return value r1 is one interation PageRank value for the input node.
  # Please round r1 to 2 decimal places.

  r1 = 0

  ############# Your code here ############
  ## Note:
  ## 1: You should not use nx.pagerank
  #########################################

  return r1

beta = 0.8
r0 = 1 / G_karate.number_of_nodes()
node = 0
r1 = one_iter_pagerank(G_karate, beta, r0, node)
print("The PageRank value for node 0 after one iteration is {}".format(r1))

The PageRank value for node 0 after one iteration is 0

8.2.2.5. Question 4: What is the (raw) closeness centrality for the karate club network node 5?

The equation for closeness centrality is \(c(v) = \frac{1}{\sum_{u \neq v}\text{shortest path length between } u \text{ and } v}\)

def closeness_centrality(G_karate, node=5):
  # TODO: Implement the function that calculates closeness centrality
  # for a node in karate club network. G is the input karate club
  # network and node is the node id in the graph. Please round the
  # closeness centrality result to 2 decimal places.

  closeness = 0

  ## Note:
  ## 1: You can use networkx closeness centrality function.
  ## 2: Notice that networkx closeness centrality returns the normalized
  ## closeness directly, which is different from the raw (unnormalized)
  ## one that we learned in the lecture.
  #########################################

  return closeness

node = 5
closeness = closeness_centrality(G_karate, node=node)
print("The node 5 has closeness centrality {}".format(closeness))

The node 5 has closeness centrality 0

8.3. Graph to Tensor

We will then work together to transform the graph \(G\) into a PyTorch tensor, so that we can perform machine learning over the graph.

8.3.1. PyTorch Geometric Tutorial

PyTorch Geometric (PyG) is an extension library for PyTorch. It provides useful primitives to develop Graph Deep Learning models, including various graph neural network layers and a large number of benchmark datasets.

Don’t worry if you don’t understand some concepts such as GCNConv, which totally depands on what algorithms you will use further :)

This tutorial is adapted from https://colab.research.google.com/drive/1h3-vJGRVloF5zStxL5I0rSy4ZUPNsjy8?usp=sharing#scrollTo=ci-LpZWhRJoI

You can explore more PyG functions through its documentation.

import torch

print("PyTorch has version {}".format(torch.__version__))

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Cell In[17], line 1
----> 1 import torch
      3 print("PyTorch has version {}".format(torch.__version__))

ModuleNotFoundError: No module named 'torch'

8.3.1.1. Installing dependencies

The installation of PyG on Colab can be a little bit tricky. Execute the cell below – in case of issues, more information can be found on the PyG’s installation page.

Note: This cell might take a while (up to ~30 minutes) to run

# Install torch geometric
!pip install -q torch-scatter -f https://pytorch-geometric.com/whl/torch-1.7.0+cu101.html
!pip install -q torch-sparse -f https://pytorch-geometric.com/whl/torch-1.7.0+cu101.html
!pip install -q torch-geometric

?25l     ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 0.0/108.0 kB ? eta -:--:--
     ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 108.0/108.0 kB 3.7 MB/s eta 0:00:00
?25h  Preparing metadata (setup.py) ... ?25l?25hdone
  Building wheel for torch-scatter (setup.py) ... ?25l?25hdone
     ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 210.0/210.0 kB 5.3 MB/s eta 0:00:00
?25h  Preparing metadata (setup.py) ... ?25l?25hdone
  Building wheel for torch-sparse (setup.py) ... ?25l?25hdone
     ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 64.2/64.2 kB 2.2 MB/s eta 0:00:00
   ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 1.1/1.1 MB 23.0 MB/s eta 0:00:00
?25h

8.3.1.2. PyTorch tensor basics

Recently, deep learning on graphs has emerged to one of the hottest research fields in the deep learning community. Here, Graph Neural Networks (GNNs) aim to generalize classical deep learning concepts to irregular structured data (in contrast to images or texts) and to enable neural networks to reason about objects and their relations.

This tutorial will introduce you to some fundamental concepts regarding deep learning on graphs via Graph Neural Networks based on the PyTorch Geometric (PyG) library. PyTorch Geometric is an extension library to the popular deep learning framework PyTorch, and consists of various methods and utilities to ease the implementation of Graph Neural Networks.

We can generate PyTorch tensor with all zeros, ones or random values.

# Generate 3 x 4 tensor with all ones
ones = torch.ones(3, 4)
print(ones)

# Generate 3 x 4 tensor with all zeros
zeros = torch.zeros(3, 4)
print(zeros)

# Generate 3 x 4 tensor with random values on the interval [0, 1)
random_tensor = torch.rand(3, 4)
print(random_tensor)

# Get the shape of the tensor
print(ones.shape)

tensor([[1., 1., 1., 1.],
        [1., 1., 1., 1.],
        [1., 1., 1., 1.]])
tensor([[0., 0., 0., 0.],
        [0., 0., 0., 0.],
        [0., 0., 0., 0.]])
tensor([[0.4820, 0.1941, 0.8239, 0.8437],
        [0.3316, 0.3270, 0.7687, 0.9182],
        [0.1079, 0.0475, 0.0798, 0.3385]])
torch.Size([3, 4])

PyTorch tensor contains elements for a single data type, the dtype.

# Create a 3 x 4 tensor with all 32-bit floating point zeros
zeros = torch.zeros(3, 4, dtype=torch.float32)
print(zeros.dtype)

# Change the tensor dtype to 64-bit integer
zeros = zeros.type(torch.long)
print(zeros.dtype)

torch.float32
torch.int64

8.3.1.3. Dataset

Following Kipf et al. (2017), let’s dive into the world of GNNs by looking at a simple graph-structured and previous example that we used, the well-known Zachary’s karate club network. Here, we are interested in detecting communities that arise from the member’s interaction.

PyTorch Geometric provides an easy access to the dataset via the torch_geometric.datasets subpackage:

from torch_geometric.datasets import KarateClub

dataset = KarateClub()
print(f'Dataset: {dataset}:')
print('======================')
print(f'Number of graphs: {len(dataset)}')
print(f'Number of features: {dataset.num_features}')
print(f'Number of classes: {dataset.num_classes}')

Dataset: KarateClub():
======================
Number of graphs: 1
Number of features: 34
Number of classes: 4

After initializing the KarateClub dataset, we first can inspect some of its properties. For example, we can see that this dataset holds exactly one graph, and that each node in this dataset is assigned a 34-dimensional feature vector (which uniquely describes the members of the karate club). Furthermore, the graph holds exactly 4 classes, which represent the community each node belongs to.

Let’s now look at the underlying graph in more detail:

data = dataset[0]  # Get the first graph object.

print(data)
print('==============================================================')

# Gather some statistics about the graph.
print(f'Number of nodes: {data.num_nodes}')
print(f'Number of edges: {data.num_edges}')
print(f'Average node degree: {(data.num_edges) / data.num_nodes:.2f}')
print(f'Number of training nodes: {data.train_mask.sum()}')
print(f'Training node label rate: {int(data.train_mask.sum()) / data.num_nodes:.2f}')
print(f'Contains isolated nodes: {data.has_isolated_nodes()}')
print(f'Contains self-loops: {data.has_self_loops()}')
print(f'Is undirected: {data.is_undirected()}')

Data(x=[34, 34], edge_index=[2, 156], y=[34], train_mask=[34])
==============================================================
Number of nodes: 34
Number of edges: 156
Average node degree: 4.59
Number of training nodes: 4
Training node label rate: 0.12
Contains isolated nodes: False
Contains self-loops: False
Is undirected: True

data.edge_index.T

tensor([[ 0,  1],
        [ 0,  2],
        [ 0,  3],
        [ 0,  4],
        [ 0,  5],
        [ 0,  6],
        [ 0,  7],
        [ 0,  8],
        [ 0, 10],
        [ 0, 11],
        [ 0, 12],
        [ 0, 13],
        [ 0, 17],
        [ 0, 19],
        [ 0, 21],
        [ 0, 31],
        [ 1,  0],
        [ 1,  2],
        [ 1,  3],
        [ 1,  7],
        [ 1, 13],
        [ 1, 17],
        [ 1, 19],
        [ 1, 21],
        [ 1, 30],
        [ 2,  0],
        [ 2,  1],
        [ 2,  3],
        [ 2,  7],
        [ 2,  8],
        [ 2,  9],
        [ 2, 13],
        [ 2, 27],
        [ 2, 28],
        [ 2, 32],
        [ 3,  0],
        [ 3,  1],
        [ 3,  2],
        [ 3,  7],
        [ 3, 12],
        [ 3, 13],
        [ 4,  0],
        [ 4,  6],
        [ 4, 10],
        [ 5,  0],
        [ 5,  6],
        [ 5, 10],
        [ 5, 16],
        [ 6,  0],
        [ 6,  4],
        [ 6,  5],
        [ 6, 16],
        [ 7,  0],
        [ 7,  1],
        [ 7,  2],
        [ 7,  3],
        [ 8,  0],
        [ 8,  2],
        [ 8, 30],
        [ 8, 32],
        [ 8, 33],
        [ 9,  2],
        [ 9, 33],
        [10,  0],
        [10,  4],
        [10,  5],
        [11,  0],
        [12,  0],
        [12,  3],
        [13,  0],
        [13,  1],
        [13,  2],
        [13,  3],
        [13, 33],
        [14, 32],
        [14, 33],
        [15, 32],
        [15, 33],
        [16,  5],
        [16,  6],
        [17,  0],
        [17,  1],
        [18, 32],
        [18, 33],
        [19,  0],
        [19,  1],
        [19, 33],
        [20, 32],
        [20, 33],
        [21,  0],
        [21,  1],
        [22, 32],
        [22, 33],
        [23, 25],
        [23, 27],
        [23, 29],
        [23, 32],
        [23, 33],
        [24, 25],
        [24, 27],
        [24, 31],
        [25, 23],
        [25, 24],
        [25, 31],
        [26, 29],
        [26, 33],
        [27,  2],
        [27, 23],
        [27, 24],
        [27, 33],
        [28,  2],
        [28, 31],
        [28, 33],
        [29, 23],
        [29, 26],
        [29, 32],
        [29, 33],
        [30,  1],
        [30,  8],
        [30, 32],
        [30, 33],
        [31,  0],
        [31, 24],
        [31, 25],
        [31, 28],
        [31, 32],
        [31, 33],
        [32,  2],
        [32,  8],
        [32, 14],
        [32, 15],
        [32, 18],
        [32, 20],
        [32, 22],
        [32, 23],
        [32, 29],
        [32, 30],
        [32, 31],
        [32, 33],
        [33,  8],
        [33,  9],
        [33, 13],
        [33, 14],
        [33, 15],
        [33, 18],
        [33, 19],
        [33, 20],
        [33, 22],
        [33, 23],
        [33, 26],
        [33, 27],
        [33, 28],
        [33, 29],
        [33, 30],
        [33, 31],
        [33, 32]])

8.3.1.4. Data

Each graph in PyTorch Geometric is represented by a single Data object, which holds all the information to describe its graph representation. We can print the data object anytime via print(data) to receive a short summary about its attributes and their shapes:

print(data)

Data(x=[34, 34], edge_index=[2, 156], y=[34], train_mask=[34])

We can see that this data object holds 4 attributes: (1) The edge_index property holds the information about the graph connectivity, i.e., a tuple of source and destination node indices for each edge. PyG further refers to (2) node features as x (each of the 34 nodes is assigned a 34-dim feature vector), and to (3) node labels as y (each node is assigned to exactly one class). (4) There also exists an additional attribute called train_mask, which describes for which nodes we already know their community assigments. In total, we are only aware of the ground-truth labels of 4 nodes (one for each community), and the task is to infer the community assignment for the remaining nodes.

The data object also provides some utility functions to infer some basic properties of the underlying graph. For example, we can easily infer whether there exists isolated nodes in the graph (i.e. there exists no edge to any node), whether the graph contains self-loops (i.e., \((v, v) \in \mathbb{E}\)), or whether the graph is undirected (i.e., for each edge \((v, w) \in \mathbb{E}\) there also exists the edge \((w, v) \in \mathbb{E}\)).

8.3.1.5. Edge Index

Next we’ll print the edge_index of our graph:

from IPython.display import Javascript  # Restrict height of output cell.
display(Javascript('''google.colab.output.setIframeHeight(0, true, {maxHeight: 300})'''))

edge_index = data.edge_index
print(edge_index.t())

tensor([[ 0,  1],
        [ 0,  2],
        [ 0,  3],
        [ 0,  4],
        [ 0,  5],
        [ 0,  6],
        [ 0,  7],
        [ 0,  8],
        [ 0, 10],
        [ 0, 11],
        [ 0, 12],
        [ 0, 13],
        [ 0, 17],
        [ 0, 19],
        [ 0, 21],
        [ 0, 31],
        [ 1,  0],
        [ 1,  2],
        [ 1,  3],
        [ 1,  7],
        [ 1, 13],
        [ 1, 17],
        [ 1, 19],
        [ 1, 21],
        [ 1, 30],
        [ 2,  0],
        [ 2,  1],
        [ 2,  3],
        [ 2,  7],
        [ 2,  8],
        [ 2,  9],
        [ 2, 13],
        [ 2, 27],
        [ 2, 28],
        [ 2, 32],
        [ 3,  0],
        [ 3,  1],
        [ 3,  2],
        [ 3,  7],
        [ 3, 12],
        [ 3, 13],
        [ 4,  0],
        [ 4,  6],
        [ 4, 10],
        [ 5,  0],
        [ 5,  6],
        [ 5, 10],
        [ 5, 16],
        [ 6,  0],
        [ 6,  4],
        [ 6,  5],
        [ 6, 16],
        [ 7,  0],
        [ 7,  1],
        [ 7,  2],
        [ 7,  3],
        [ 8,  0],
        [ 8,  2],
        [ 8, 30],
        [ 8, 32],
        [ 8, 33],
        [ 9,  2],
        [ 9, 33],
        [10,  0],
        [10,  4],
        [10,  5],
        [11,  0],
        [12,  0],
        [12,  3],
        [13,  0],
        [13,  1],
        [13,  2],
        [13,  3],
        [13, 33],
        [14, 32],
        [14, 33],
        [15, 32],
        [15, 33],
        [16,  5],
        [16,  6],
        [17,  0],
        [17,  1],
        [18, 32],
        [18, 33],
        [19,  0],
        [19,  1],
        [19, 33],
        [20, 32],
        [20, 33],
        [21,  0],
        [21,  1],
        [22, 32],
        [22, 33],
        [23, 25],
        [23, 27],
        [23, 29],
        [23, 32],
        [23, 33],
        [24, 25],
        [24, 27],
        [24, 31],
        [25, 23],
        [25, 24],
        [25, 31],
        [26, 29],
        [26, 33],
        [27,  2],
        [27, 23],
        [27, 24],
        [27, 33],
        [28,  2],
        [28, 31],
        [28, 33],
        [29, 23],
        [29, 26],
        [29, 32],
        [29, 33],
        [30,  1],
        [30,  8],
        [30, 32],
        [30, 33],
        [31,  0],
        [31, 24],
        [31, 25],
        [31, 28],
        [31, 32],
        [31, 33],
        [32,  2],
        [32,  8],
        [32, 14],
        [32, 15],
        [32, 18],
        [32, 20],
        [32, 22],
        [32, 23],
        [32, 29],
        [32, 30],
        [32, 31],
        [32, 33],
        [33,  8],
        [33,  9],
        [33, 13],
        [33, 14],
        [33, 15],
        [33, 18],
        [33, 19],
        [33, 20],
        [33, 22],
        [33, 23],
        [33, 26],
        [33, 27],
        [33, 28],
        [33, 29],
        [33, 30],
        [33, 31],
        [33, 32]])

By printing edge_index, we can further understand how PyG represents graph connectivity internally. We can see that for each edge, edge_index holds a tuple of two node indices, where the first value describes the node index of the source node and the second value describes the node index of the destination node of an edge.

This representation is known as the COO format (coordinate format) commonly used for representing sparse matrices. Instead of holding the adjacency information in a dense representation \(\mathbf{A} \in \{ 0, 1 \}^{|\mathbb{V}| \times |\mathbb{V}|}\), PyG represents graphs sparsely, which refers to only holding the coordinates/values for which entries in \(\mathbf{A}\) are non-zero.

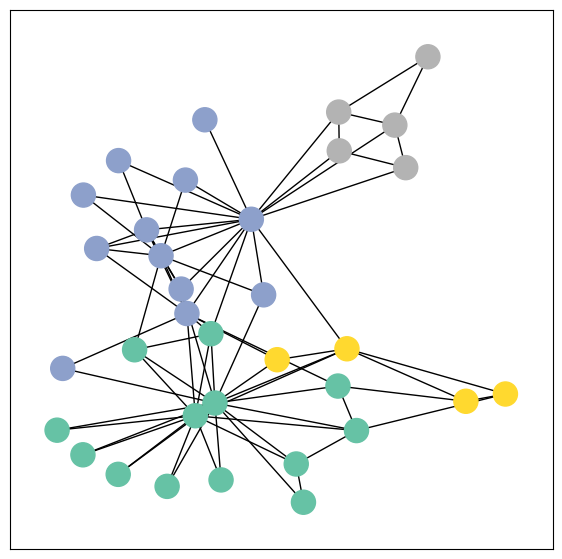
We can further visualize the graph by converting it to the networkx library format, which implements, in addition to graph manipulation functionalities, powerful tools for visualization:

# Helper function for visualization.
%matplotlib inline
import torch
import networkx as nx
import matplotlib.pyplot as plt

# Visualization function for NX graph or PyTorch tensor
def visualize(h, color, epoch=None, loss=None, accuracy=None):
    plt.figure(figsize=(7,7))
    plt.xticks([])
    plt.yticks([])

    if torch.is_tensor(h):
        h = h.detach().cpu().numpy()
        plt.scatter(h[:, 0], h[:, 1], s=140, c=color, cmap="Set2")
        if epoch is not None and loss is not None and accuracy['train'] is not None and accuracy['val'] is not None:
            plt.xlabel((f'Epoch: {epoch}, Loss: {loss.item():.4f} \n'
                       f'Training Accuracy: {accuracy["train"]*100:.2f}% \n'
                       f' Validation Accuracy: {accuracy["val"]*100:.2f}%'),
                       fontsize=16)
    else:
        nx.draw_networkx(h, pos=nx.spring_layout(h, seed=42), with_labels=False,
                         node_color=color, cmap="Set2")
    plt.show()

from torch_geometric.utils import to_networkx

G = to_networkx(data, to_undirected=True)
visualize(G, color=data.y)

8.3.2. Exercise

8.3.2.1. Question 5: Get the edge list of the karate club network and transform it into torch.LongTensor. What is the torch.sum value of pos_edge_index tensor?

def graph_to_edge_list(G_karate):
  # TODO: Implement the function that returns the edge list of
  # an nx.Graph. The returned edge_list should be a list of tuples
  # where each tuple is a tuple representing an edge connected
  # by two nodes.

  edge_list = []

  ############# Your code here ############
  #########################################

  return edge_list

def edge_list_to_tensor(edge_list):
  # TODO: Implement the function that transforms the edge_list to
  # tensor. The input edge_list is a list of tuples and the resulting
  # tensor should have the shape [2, len(edge_list)].

  edge_index = torch.tensor([])

  ############# Your code here ############
  #########################################

  return edge_index

pos_edge_list = graph_to_edge_list(G_karate)
pos_edge_index = edge_list_to_tensor(pos_edge_list)
print("The pos_edge_index tensor has shape {}".format(pos_edge_index.shape))
print("The pos_edge_index tensor has sum value {}".format(torch.sum(pos_edge_index)))

The pos_edge_index tensor has shape torch.Size([2, 78])
The pos_edge_index tensor has sum value 2535

8.3.2.2. Question 6: Please implement following function that samples negative edges. Then answer which edges (edge_1 to edge_5) are the negative edges in the karate club network?

“Negative” edges refer to the edges/links that do not exist in the graph. The term “negative” is borrowed from “negative sampling” in link prediction. It has nothing to do with the edge weights.

For example, given an edge (src, dst), you should check that neither (src, dst) nor (dst, src) are edges in the Graph. If these hold true, then it is a negative edge.

import random

def sample_negative_edges(G_karate, num_neg_samples):
  # TODO: Implement the function that returns a list of negative edges.
  # The number of sampled negative edges is num_neg_samples. You do not
  # need to consider the corner case when the number of possible negative edges
  # is less than num_neg_samples. It should be ok as long as your implementation
  # works on the karate club network. In this implementation, self loops should
  # not be considered as either a positive or negative edge. Also, notice that
  # the karate club network is an undirected graph, if (0, 1) is a positive
  # edge, do you think (1, 0) can be a negative one?

  neg_edge_list = []

  ############# Your code here ############
  #########################################

  return neg_edge_list

# Sample 78 negative edges
neg_edge_list = sample_negative_edges(G_karate, len(pos_edge_list))

# Transform the negative edge list to tensor
neg_edge_index = edge_list_to_tensor(neg_edge_list)
print("The neg_edge_index tensor has shape {}".format(neg_edge_index.shape))

# Which of following edges can be negative ones?
edge_1 = (7, 1)
edge_2 = (1, 33)
edge_3 = (33, 22)
edge_4 = (0, 4)
edge_5 = (4, 2)

############# Your code here ############
## Note:
## 1: For each of the 5 edges, print whether it can be negative edge
#########################################

The neg_edge_index tensor has shape torch.Size([2, 78])
No
Yes
No
No
Yes

8.4. Node Emebedding Learning

Now, we will finish the first learning algorithm on graphs: a node embedding model.

8.4.1. Setup

import torch
import torch.nn as nn
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA

print(torch.__version__)

2.4.0+cu121

To write our own node embedding learning methods, we’ll heavily use the nn.Embedding module in PyTorch. Let’s see how to use nn.Embedding:

# Initialize an embedding layer
# Suppose we want to have embedding for 4 items (e.g., nodes)
# Each item is represented with 8 dimensional vector

emb_sample = nn.Embedding(num_embeddings=4, embedding_dim=8)
print('Sample embedding layer: {}'.format(emb_sample))

Sample embedding layer: Embedding(4, 8)

We can select items from the embedding matrix, by using Tensor indices

# Select an embedding in emb_sample
id = torch.LongTensor([1])
print(emb_sample(id))

# Select multiple embeddings
ids = torch.LongTensor([1, 3])
print(emb_sample(ids))

# Get the shape of the embedding weight matrix
shape = emb_sample.weight.data.shape
print(shape)

# Overwrite the weight to tensor with all ones
emb_sample.weight.data = torch.ones(shape)

# Let's check if the emb is indeed initilized
ids = torch.LongTensor([0, 3])
print(emb_sample(ids))

tensor([[ 0.0101,  0.8362,  1.2051, -0.0683, -0.4875, -0.4971,  1.4690,  0.0375]],
       grad_fn=<EmbeddingBackward0>)
tensor([[ 0.0101,  0.8362,  1.2051, -0.0683, -0.4875, -0.4971,  1.4690,  0.0375],
        [ 0.6357, -0.7775, -0.0557, -0.0443,  2.0859,  0.1051,  0.0199, -0.6802]],
       grad_fn=<EmbeddingBackward0>)
torch.Size([4, 8])
tensor([[1., 1., 1., 1., 1., 1., 1., 1.],
        [1., 1., 1., 1., 1., 1., 1., 1.]], grad_fn=<EmbeddingBackward0>)

8.4.2. Exercise

8.4.2.1. Question 7: Following the below requirements, please create the node embedding matrix

Now, it’s your time to create node embedding matrix for the graph we have!

• We want to have 16 dimensional vector for each node in the karate club network.

• We want to initalize the matrix under uniform distribution, in the range of \([0, 1)\). We suggest you using torch.rand.

# Please do not change / reset the random seed
torch.manual_seed(1)

def create_node_emb(num_node=34, embedding_dim=16):
  # TODO: Implement this function that will create the node embedding matrix.
  # A torch.nn.Embedding layer will be returned. You do not need to change
  # the values of num_node and embedding_dim. The weight matrix of returned
  # layer should be initialized under uniform distribution.

  emb = None

  ############# Your code here ############
  #########################################

  return emb

emb = create_node_emb()
ids = torch.LongTensor([0, 3])

# Print the embedding layer
print("Embedding: {}".format(emb))

# An example that gets the embeddings for node 0 and 3
print(emb(ids))

Embedding: Embedding(34, 16)
tensor([[0.2114, 0.7335, 0.1433, 0.9647, 0.2933, 0.7951, 0.5170, 0.2801, 0.8339,
         0.1185, 0.2355, 0.5599, 0.8966, 0.2858, 0.1955, 0.1808],
        [0.7486, 0.6546, 0.3843, 0.9820, 0.6012, 0.3710, 0.4929, 0.9915, 0.8358,
         0.4629, 0.9902, 0.7196, 0.2338, 0.0450, 0.7906, 0.9689]],
       grad_fn=<EmbeddingBackward0>)

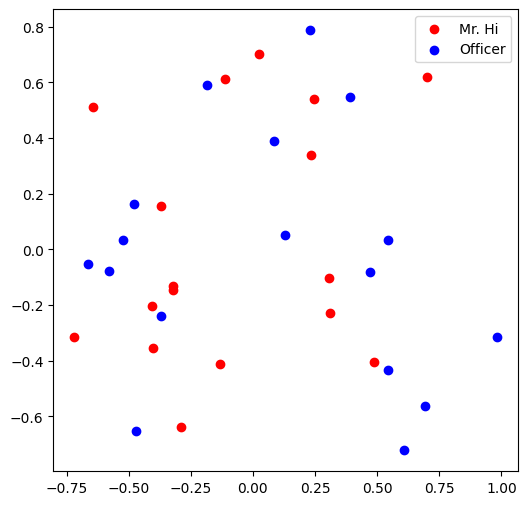
8.4.2.2. Question 8: Visualize the initial node embeddings

One good way to understand an embedding matrix, is to visualize it in a 2D space. Here, we have implemented an embedding visualization function for you. We first do PCA to reduce the dimensionality of embeddings to a 2D space. Then we visualize each point, colored by the community it belongs to.

def visualize_emb(emb):
  X = emb.weight.data.numpy()
  pca = PCA(n_components=2)
  components = pca.fit_transform(X)
  plt.figure(figsize=(6, 6))
  club1_x = []
  club1_y = []
  club2_x = []
  club2_y = []

  ############# Your code here ############
  ## Note:
  ## 1: You need to visualize each node's club (i.e. "Mr. Hi" or "Officer")
  #########################################

  plt.scatter(club1_x, club1_y, color="red", label="Mr. Hi")
  plt.scatter(club2_x, club2_y, color="blue", label="Officer")
  plt.legend()
  plt.show()

# Visualize the initial random embeddding
visualize_emb(emb)

8.4.2.3. Question 9: Training the embedding! What is the best performance you can get? Please report both the best loss and accuracy on Gradescope.

We want to optimize our embeddings for the task of classifying edges as positive or negative. Given an edge and the embeddings for each node, the dot product of the embeddings, followed by a sigmoid, should give us the likelihood of that edge being either positive (output of sigmoid > 0.5) or negative (output of sigmoid < 0.5).

Note that we’re using the functions you wrote in the previous questions, as well as the variables initialized in previous cells. If you’re running into issues, make sure your answers to questions 1-6 are correct.

from torch.optim import SGD
import torch.nn as nn

def accuracy(pred, label):
  # TODO: Implement the accuracy function. This function takes the
  # pred tensor (the resulting tensor after sigmoid) and the label
  # tensor (torch.LongTensor). Predicted value greater than 0.5 will
  # be classified as label 1. Else it will be classified as label 0.
  # The returned accuracy should be rounded to 4 decimal places.
  # For example, accuracy 0.82956 will be rounded to 0.8296.

  accu = 0.0

  ############# Your code here ############
  #########################################

  return accu

def train(emb, loss_fn, sigmoid, train_label, train_edge):
  # TODO: Train the embedding layer here. You can also change epochs and
  # learning rate. In general, you need to implement:
  # (1) Get the embeddings of the nodes in train_edge
  # (2) Dot product the embeddings between each node pair
  # (3) Feed the dot product result into sigmoid
  # (4) Feed the sigmoid output into the loss_fn
  # (5) Print both loss and accuracy of each epoch
  # (6) Update the embeddings using the loss and optimizer
  # (as a sanity check, the loss should decrease during training)

  epochs = 500
  learning_rate = 0.1

  optimizer = SGD(emb.parameters(), lr=learning_rate, momentum=0.9)

  for i in range(epochs):

    ############# Your code here ############
    #########################################

loss_fn = nn.BCELoss()
sigmoid = nn.Sigmoid()

print(pos_edge_index.shape)

# Generate the positive and negative labels
pos_label = torch.ones(pos_edge_index.shape[1], )
neg_label = torch.zeros(neg_edge_index.shape[1], )

# Concat positive and negative labels into one tensor
train_label = torch.cat([pos_label, neg_label], dim=0)

# Concat positive and negative edges into one tensor
# Since the network is very small, we do not split the edges into val/test sets
train_edge = torch.cat([pos_edge_index, neg_edge_index], dim=1)
print(train_edge.shape)

train(emb, loss_fn, sigmoid, train_label, train_edge)

torch.Size([2, 78])
torch.Size([2, 156])
Epoch: 0 Loss: 2.0010430812835693 Acc: 0.5
Epoch: 1 Loss: 1.9884600639343262 Acc: 0.5
Epoch: 2 Loss: 1.964735984802246 Acc: 0.5
Epoch: 3 Loss: 1.931316614151001 Acc: 0.5
Epoch: 4 Loss: 1.8896243572235107 Acc: 0.5
Epoch: 5 Loss: 1.841033935546875 Acc: 0.5
Epoch: 6 Loss: 1.7868558168411255 Acc: 0.5
Epoch: 7 Loss: 1.7283258438110352 Acc: 0.5
Epoch: 8 Loss: 1.6665958166122437 Acc: 0.5
Epoch: 9 Loss: 1.6027268171310425 Acc: 0.5
Epoch: 10 Loss: 1.5376862287521362 Acc: 0.5
Epoch: 11 Loss: 1.4723446369171143 Acc: 0.5
Epoch: 12 Loss: 1.407472848892212 Acc: 0.5
Epoch: 13 Loss: 1.343743085861206 Acc: 0.5
Epoch: 14 Loss: 1.2817271947860718 Acc: 0.5
Epoch: 15 Loss: 1.221899151802063 Acc: 0.5
Epoch: 16 Loss: 1.1646374464035034 Acc: 0.5
Epoch: 17 Loss: 1.1102285385131836 Acc: 0.5
Epoch: 18 Loss: 1.0588724613189697 Acc: 0.5
Epoch: 19 Loss: 1.0106909275054932 Acc: 0.5
Epoch: 20 Loss: 0.9657337665557861 Acc: 0.5
Epoch: 21 Loss: 0.9239897131919861 Acc: 0.5064102411270142
Epoch: 22 Loss: 0.8853950500488281 Acc: 0.5064102411270142
Epoch: 23 Loss: 0.8498445153236389 Acc: 0.5064102411270142
Epoch: 24 Loss: 0.8172003626823425 Acc: 0.5
Epoch: 25 Loss: 0.7873010635375977 Acc: 0.5064102411270142
Epoch: 26 Loss: 0.7599697709083557 Acc: 0.5192307829856873
Epoch: 27 Loss: 0.7350209951400757 Acc: 0.5320512652397156
Epoch: 28 Loss: 0.7122665643692017 Acc: 0.5384615659713745
Epoch: 29 Loss: 0.6915203928947449 Acc: 0.5512820482254028
Epoch: 30 Loss: 0.6726014614105225 Acc: 0.557692289352417
Epoch: 31 Loss: 0.6553373336791992 Acc: 0.557692289352417
Epoch: 32 Loss: 0.6395652890205383 Acc: 0.5705128312110901
Epoch: 33 Loss: 0.625133752822876 Acc: 0.6089743375778198
Epoch: 34 Loss: 0.61190265417099 Acc: 0.6153846383094788
Epoch: 35 Loss: 0.5997437238693237 Acc: 0.6089743375778198
Epoch: 36 Loss: 0.5885403156280518 Acc: 0.6217948794364929
Epoch: 37 Loss: 0.5781866312026978 Acc: 0.6410256624221802
Epoch: 38 Loss: 0.5685875415802002 Acc: 0.6666666865348816
Epoch: 39 Loss: 0.5596577525138855 Acc: 0.7051281929016113
Epoch: 40 Loss: 0.5513209104537964 Acc: 0.7243589758872986
Epoch: 41 Loss: 0.5435088872909546 Acc: 0.7307692170143127
Epoch: 42 Loss: 0.5361612439155579 Acc: 0.7435897588729858
Epoch: 43 Loss: 0.5292242169380188 Acc: 0.75
Epoch: 44 Loss: 0.5226502418518066 Acc: 0.7628205418586731
Epoch: 45 Loss: 0.5163971185684204 Acc: 0.7628205418586731
Epoch: 46 Loss: 0.5104278326034546 Acc: 0.7756410241127014
Epoch: 47 Loss: 0.5047093629837036 Acc: 0.7948718070983887
Epoch: 48 Loss: 0.4992128908634186 Acc: 0.8012820482254028
Epoch: 49 Loss: 0.4939127564430237 Acc: 0.807692289352417
Epoch: 50 Loss: 0.4887866973876953 Acc: 0.8205128312110901
Epoch: 51 Loss: 0.48381468653678894 Acc: 0.8205128312110901
Epoch: 52 Loss: 0.4789794981479645 Acc: 0.8205128312110901
Epoch: 53 Loss: 0.47426581382751465 Acc: 0.8333333134651184
Epoch: 54 Loss: 0.4696601927280426 Acc: 0.8397436141967773
Epoch: 55 Loss: 0.4651508927345276 Acc: 0.8461538553237915
Epoch: 56 Loss: 0.46072760224342346 Acc: 0.8525640964508057
Epoch: 57 Loss: 0.456381231546402 Acc: 0.8589743375778198
Epoch: 58 Loss: 0.45210394263267517 Acc: 0.8653846383094788
Epoch: 59 Loss: 0.44788870215415955 Acc: 0.8782051205635071
Epoch: 60 Loss: 0.44372960925102234 Acc: 0.8910256624221802
Epoch: 61 Loss: 0.43962129950523376 Acc: 0.8910256624221802
Epoch: 62 Loss: 0.43555939197540283 Acc: 0.8974359035491943
Epoch: 63 Loss: 0.43153974413871765 Acc: 0.8974359035491943
Epoch: 64 Loss: 0.427558958530426 Acc: 0.9038461446762085
Epoch: 65 Loss: 0.4236142635345459 Acc: 0.9038461446762085
Epoch: 66 Loss: 0.4197029173374176 Acc: 0.9038461446762085
Epoch: 67 Loss: 0.41582298278808594 Acc: 0.9038461446762085
Epoch: 68 Loss: 0.41197243332862854 Acc: 0.9102563858032227
Epoch: 69 Loss: 0.4081498980522156 Acc: 0.9102563858032227
Epoch: 70 Loss: 0.4043539762496948 Acc: 0.9102563858032227
Epoch: 71 Loss: 0.4005836844444275 Acc: 0.9102563858032227
Epoch: 72 Loss: 0.39683812856674194 Acc: 0.9166666865348816
Epoch: 73 Loss: 0.39311665296554565 Acc: 0.9166666865348816
Epoch: 74 Loss: 0.38941866159439087 Acc: 0.9166666865348816
Epoch: 75 Loss: 0.3857438862323761 Acc: 0.9166666865348816
Epoch: 76 Loss: 0.3820918798446655 Acc: 0.9230769276618958
Epoch: 77 Loss: 0.37846261262893677 Acc: 0.9230769276618958
Epoch: 78 Loss: 0.3748558759689331 Acc: 0.9230769276618958
Epoch: 79 Loss: 0.3712717592716217 Acc: 0.9294871687889099
Epoch: 80 Loss: 0.3677101731300354 Acc: 0.9294871687889099
Epoch: 81 Loss: 0.3641713857650757 Acc: 0.9294871687889099
Epoch: 82 Loss: 0.36065542697906494 Acc: 0.9294871687889099
Epoch: 83 Loss: 0.3571624755859375 Acc: 0.9294871687889099
Epoch: 84 Loss: 0.35369282960891724 Acc: 0.9294871687889099
Epoch: 85 Loss: 0.35024669766426086 Acc: 0.9294871687889099
Epoch: 86 Loss: 0.3468242883682251 Acc: 0.9294871687889099
Epoch: 87 Loss: 0.3434259593486786 Acc: 0.9294871687889099
Epoch: 88 Loss: 0.34005188941955566 Acc: 0.9358974099159241
Epoch: 89 Loss: 0.33670246601104736 Acc: 0.9358974099159241
Epoch: 90 Loss: 0.3333779275417328 Acc: 0.942307710647583
Epoch: 91 Loss: 0.3300785422325134 Acc: 0.942307710647583
Epoch: 92 Loss: 0.32680460810661316 Acc: 0.942307710647583
Epoch: 93 Loss: 0.32355639338493347 Acc: 0.942307710647583
Epoch: 94 Loss: 0.3203341066837311 Acc: 0.942307710647583
Epoch: 95 Loss: 0.31713807582855225 Acc: 0.942307710647583
Epoch: 96 Loss: 0.31396856904029846 Acc: 0.942307710647583
Epoch: 97 Loss: 0.3108256757259369 Acc: 0.942307710647583
Epoch: 98 Loss: 0.3077096939086914 Acc: 0.942307710647583
Epoch: 99 Loss: 0.30462074279785156 Acc: 0.942307710647583
Epoch: 100 Loss: 0.3015589714050293 Acc: 0.942307710647583
Epoch: 101 Loss: 0.2985246479511261 Acc: 0.942307710647583
Epoch: 102 Loss: 0.29551777243614197 Acc: 0.942307710647583
Epoch: 103 Loss: 0.29253849387168884 Acc: 0.942307710647583
Epoch: 104 Loss: 0.28958696126937866 Acc: 0.942307710647583
Epoch: 105 Loss: 0.28666314482688904 Acc: 0.9487179517745972
Epoch: 106 Loss: 0.2837671935558319 Acc: 0.9487179517745972
Epoch: 107 Loss: 0.2808990180492401 Acc: 0.9487179517745972
Epoch: 108 Loss: 0.2780587375164032 Acc: 0.9487179517745972
Epoch: 109 Loss: 0.2752462923526764 Acc: 0.9551281929016113
Epoch: 110 Loss: 0.2724616229534149 Acc: 0.9551281929016113
Epoch: 111 Loss: 0.26970475912094116 Acc: 0.9551281929016113
Epoch: 112 Loss: 0.26697561144828796 Acc: 0.9551281929016113
Epoch: 113 Loss: 0.26427412033081055 Acc: 0.9551281929016113
Epoch: 114 Loss: 0.26160016655921936 Acc: 0.9551281929016113
Epoch: 115 Loss: 0.25895363092422485 Acc: 0.9551281929016113
Epoch: 116 Loss: 0.25633442401885986 Acc: 0.9551281929016113
Epoch: 117 Loss: 0.2537424564361572 Acc: 0.9551281929016113
Epoch: 118 Loss: 0.25117751955986023 Acc: 0.9551281929016113
Epoch: 119 Loss: 0.24863947927951813 Acc: 0.9615384340286255
Epoch: 120 Loss: 0.24612820148468018 Acc: 0.9615384340286255
Epoch: 121 Loss: 0.24364344775676727 Acc: 0.9615384340286255
Epoch: 122 Loss: 0.24118508398532867 Acc: 0.9615384340286255
Epoch: 123 Loss: 0.23875290155410767 Acc: 0.9615384340286255
Epoch: 124 Loss: 0.23634673655033112 Acc: 0.9615384340286255
Epoch: 125 Loss: 0.23396626114845276 Acc: 0.9615384340286255
Epoch: 126 Loss: 0.23161141574382782 Acc: 0.9615384340286255
Epoch: 127 Loss: 0.2292819321155548 Acc: 0.9615384340286255
Epoch: 128 Loss: 0.22697754204273224 Acc: 0.9615384340286255
Epoch: 129 Loss: 0.2246980369091034 Acc: 0.9615384340286255
Epoch: 130 Loss: 0.22244323790073395 Acc: 0.9615384340286255
Epoch: 131 Loss: 0.22021283209323883 Acc: 0.9615384340286255
Epoch: 132 Loss: 0.2180066704750061 Acc: 0.9615384340286255
Epoch: 133 Loss: 0.2158244401216507 Acc: 0.9615384340286255
Epoch: 134 Loss: 0.21366596221923828 Acc: 0.9615384340286255
Epoch: 135 Loss: 0.2115309089422226 Acc: 0.9615384340286255
Epoch: 136 Loss: 0.2094191312789917 Acc: 0.9615384340286255
Epoch: 137 Loss: 0.2073303610086441 Acc: 0.9615384340286255
Epoch: 138 Loss: 0.20526431500911713 Acc: 0.9679487347602844
Epoch: 139 Loss: 0.20322081446647644 Acc: 0.9679487347602844
Epoch: 140 Loss: 0.20119960606098175 Acc: 0.9679487347602844
Epoch: 141 Loss: 0.19920043647289276 Acc: 0.9679487347602844
Epoch: 142 Loss: 0.1972230225801468 Acc: 0.9679487347602844
Epoch: 143 Loss: 0.1952672153711319 Acc: 0.9679487347602844
Epoch: 144 Loss: 0.193332701921463 Acc: 0.9679487347602844
Epoch: 145 Loss: 0.1914193034172058 Acc: 0.9743589758872986
Epoch: 146 Loss: 0.18952679634094238 Acc: 0.9743589758872986
Epoch: 147 Loss: 0.18765488266944885 Acc: 0.9743589758872986
Epoch: 148 Loss: 0.18580341339111328 Acc: 0.9743589758872986
Epoch: 149 Loss: 0.1839720904827118 Acc: 0.9743589758872986
Epoch: 150 Loss: 0.18216075003147125 Acc: 0.9743589758872986
Epoch: 151 Loss: 0.18036913871765137 Acc: 0.9743589758872986
Epoch: 152 Loss: 0.17859706282615662 Acc: 0.9743589758872986
Epoch: 153 Loss: 0.1768442988395691 Acc: 0.9807692170143127
Epoch: 154 Loss: 0.1751106232404709 Acc: 0.9807692170143127
Epoch: 155 Loss: 0.1733958125114441 Acc: 0.9807692170143127
Epoch: 156 Loss: 0.17169973254203796 Acc: 0.9871794581413269
Epoch: 157 Loss: 0.17002208530902863 Acc: 0.9871794581413269
Epoch: 158 Loss: 0.16836272180080414 Acc: 0.9871794581413269
Epoch: 159 Loss: 0.1667214184999466 Acc: 0.9871794581413269
Epoch: 160 Loss: 0.16509799659252167 Acc: 0.9871794581413269
Epoch: 161 Loss: 0.16349226236343384 Acc: 0.9871794581413269
Epoch: 162 Loss: 0.16190402209758759 Acc: 0.9871794581413269
Epoch: 163 Loss: 0.1603330820798874 Acc: 0.9871794581413269
Epoch: 164 Loss: 0.15877924859523773 Acc: 0.9871794581413269
Epoch: 165 Loss: 0.15724237263202667 Acc: 0.9871794581413269
Epoch: 166 Loss: 0.1557222157716751 Acc: 0.9871794581413269
Epoch: 167 Loss: 0.1542186439037323 Acc: 0.9871794581413269
Epoch: 168 Loss: 0.15273146331310272 Acc: 0.9871794581413269
Epoch: 169 Loss: 0.15126051008701324 Acc: 0.9871794581413269
Epoch: 170 Loss: 0.14980557560920715 Acc: 0.9871794581413269
Epoch: 171 Loss: 0.1483665555715561 Acc: 0.9871794581413269
Epoch: 172 Loss: 0.14694324135780334 Acc: 0.9935897588729858
Epoch: 173 Loss: 0.1455354243516922 Acc: 0.9935897588729858
Epoch: 174 Loss: 0.1441430300474167 Acc: 0.9935897588729858
Epoch: 175 Loss: 0.1427658349275589 Acc: 0.9935897588729858
Epoch: 176 Loss: 0.1414037048816681 Acc: 0.9935897588729858
Epoch: 177 Loss: 0.14005649089813232 Acc: 0.9935897588729858
Epoch: 178 Loss: 0.13872399926185608 Acc: 0.9935897588729858
Epoch: 179 Loss: 0.1374061107635498 Acc: 0.9935897588729858
Epoch: 180 Loss: 0.13610266149044037 Acc: 0.9935897588729858
Epoch: 181 Loss: 0.13481348752975464 Acc: 0.9935897588729858
Epoch: 182 Loss: 0.13353846967220306 Acc: 0.9935897588729858
Epoch: 183 Loss: 0.1322774440050125 Acc: 0.9935897588729858
Epoch: 184 Loss: 0.13103024661540985 Acc: 0.9935897588729858
Epoch: 185 Loss: 0.12979677319526672 Acc: 0.9935897588729858
Epoch: 186 Loss: 0.12857685983181 Acc: 0.9935897588729858
Epoch: 187 Loss: 0.12737035751342773 Acc: 0.9935897588729858
Epoch: 188 Loss: 0.12617714703083038 Acc: 0.9935897588729858
Epoch: 189 Loss: 0.1249970868229866 Acc: 0.9935897588729858
Epoch: 190 Loss: 0.12383002787828445 Acc: 0.9935897588729858
Epoch: 191 Loss: 0.1226758360862732 Acc: 0.9935897588729858
Epoch: 192 Loss: 0.12153439968824387 Acc: 0.9935897588729858
Epoch: 193 Loss: 0.12040555477142334 Acc: 0.9935897588729858
Epoch: 194 Loss: 0.11928918957710266 Acc: 0.9935897588729858
Epoch: 195 Loss: 0.11818517744541168 Acc: 0.9935897588729858
Epoch: 196 Loss: 0.11709340661764145 Acc: 0.9935897588729858
Epoch: 197 Loss: 0.11601369827985764 Acc: 0.9935897588729858
Epoch: 198 Loss: 0.11494597047567368 Acc: 0.9935897588729858
Epoch: 199 Loss: 0.11389008909463882 Acc: 0.9935897588729858
Epoch: 200 Loss: 0.11284591257572174 Acc: 0.9935897588729858
Epoch: 201 Loss: 0.11181335151195526 Acc: 0.9935897588729858
Epoch: 202 Loss: 0.11079225689172745 Acc: 0.9935897588729858
Epoch: 203 Loss: 0.10978250950574875 Acc: 1.0
Epoch: 204 Loss: 0.1087840124964714 Acc: 1.0
Epoch: 205 Loss: 0.10779661685228348 Acc: 1.0
Epoch: 206 Loss: 0.10682022571563721 Acc: 1.0
Epoch: 207 Loss: 0.10585474222898483 Acc: 1.0
Epoch: 208 Loss: 0.10490000247955322 Acc: 1.0
Epoch: 209 Loss: 0.10395593196153641 Acc: 1.0
Epoch: 210 Loss: 0.10302238911390305 Acc: 1.0
Epoch: 211 Loss: 0.10209929943084717 Acc: 1.0
Epoch: 212 Loss: 0.10118650645017624 Acc: 1.0
Epoch: 213 Loss: 0.10028392821550369 Acc: 1.0
Epoch: 214 Loss: 0.09939144551753998 Acc: 1.0
Epoch: 215 Loss: 0.09850896894931793 Acc: 1.0
Epoch: 216 Loss: 0.097636379301548 Acc: 1.0
Epoch: 217 Loss: 0.09677354246377945 Acc: 1.0
Epoch: 218 Loss: 0.09592039883136749 Acc: 1.0
Epoch: 219 Loss: 0.09507680684328079 Acc: 1.0
Epoch: 220 Loss: 0.09424268454313278 Acc: 1.0
Epoch: 221 Loss: 0.09341792017221451 Acc: 1.0
Epoch: 222 Loss: 0.09260240942239761 Acc: 1.0
Epoch: 223 Loss: 0.09179605543613434 Acc: 1.0
Epoch: 224 Loss: 0.09099874645471573 Acc: 1.0
Epoch: 225 Loss: 0.09021041542291641 Acc: 1.0
Epoch: 226 Loss: 0.08943092823028564 Acc: 1.0
Epoch: 227 Loss: 0.08866020292043686 Acc: 1.0
Epoch: 228 Loss: 0.0878981277346611 Acc: 1.0
Epoch: 229 Loss: 0.08714462071657181 Acc: 1.0
Epoch: 230 Loss: 0.08639959245920181 Acc: 1.0
Epoch: 231 Loss: 0.08566292375326157 Acc: 1.0
Epoch: 232 Loss: 0.0849345475435257 Acc: 1.0
Epoch: 233 Loss: 0.08421434462070465 Acc: 1.0
Epoch: 234 Loss: 0.08350224047899246 Acc: 1.0
Epoch: 235 Loss: 0.08279813081026077 Acc: 1.0
Epoch: 236 Loss: 0.08210194110870361 Acc: 1.0
Epoch: 237 Loss: 0.08141358196735382 Acc: 1.0
Epoch: 238 Loss: 0.08073293417692184 Acc: 1.0
Epoch: 239 Loss: 0.08005993813276291 Acc: 1.0
Epoch: 240 Loss: 0.07939449697732925 Acc: 1.0
Epoch: 241 Loss: 0.07873652875423431 Acc: 1.0
Epoch: 242 Loss: 0.07808593660593033 Acc: 1.0
Epoch: 243 Loss: 0.07744263857603073 Acc: 1.0
Epoch: 244 Loss: 0.07680656760931015 Acc: 1.0
Epoch: 245 Loss: 0.07617761194705963 Acc: 1.0
Epoch: 246 Loss: 0.0755557119846344 Acc: 1.0
Epoch: 247 Loss: 0.0749407634139061 Acc: 1.0
Epoch: 248 Loss: 0.07433269917964935 Acc: 1.0
Epoch: 249 Loss: 0.073731429874897 Acc: 1.0
Epoch: 250 Loss: 0.07313688844442368 Acc: 1.0
Epoch: 251 Loss: 0.07254897803068161 Acc: 1.0
Epoch: 252 Loss: 0.07196763902902603 Acc: 1.0
Epoch: 253 Loss: 0.07139278203248978 Acc: 1.0
Epoch: 254 Loss: 0.07082433253526688 Acc: 1.0
Epoch: 255 Loss: 0.07026220858097076 Acc: 1.0
Epoch: 256 Loss: 0.06970635056495667 Acc: 1.0
Epoch: 257 Loss: 0.06915665417909622 Acc: 1.0
Epoch: 258 Loss: 0.06861307471990585 Acc: 1.0
Epoch: 259 Loss: 0.06807553768157959 Acc: 1.0
Epoch: 260 Loss: 0.06754394620656967 Acc: 1.0
Epoch: 261 Loss: 0.06701825559139252 Acc: 1.0
Epoch: 262 Loss: 0.06649839133024216 Acc: 1.0
Epoch: 263 Loss: 0.06598424911499023 Acc: 1.0
Epoch: 264 Loss: 0.06547579169273376 Acc: 1.0
Epoch: 265 Loss: 0.06497295945882797 Acc: 1.0
Epoch: 266 Loss: 0.0644756555557251 Acc: 1.0
Epoch: 267 Loss: 0.06398381292819977 Acc: 1.0
Epoch: 268 Loss: 0.063497394323349 Acc: 1.0
Epoch: 269 Loss: 0.06301631033420563 Acc: 1.0
Epoch: 270 Loss: 0.06254050880670547 Acc: 1.0
Epoch: 271 Loss: 0.06206991896033287 Acc: 1.0
Epoch: 272 Loss: 0.06160446256399155 Acc: 1.0
Epoch: 273 Loss: 0.06114409491419792 Acc: 1.0
Epoch: 274 Loss: 0.06068874150514603 Acc: 1.0
Epoch: 275 Loss: 0.06023836135864258 Acc: 1.0
Epoch: 276 Loss: 0.05979287251830101 Acc: 1.0
Epoch: 277 Loss: 0.05935221537947655 Acc: 1.0
Epoch: 278 Loss: 0.058916348963975906 Acc: 1.0
Epoch: 279 Loss: 0.05848519131541252 Acc: 1.0
Epoch: 280 Loss: 0.058058690279722214 Acc: 1.0
Epoch: 281 Loss: 0.057636797428131104 Acc: 1.0
Epoch: 282 Loss: 0.057219456881284714 Acc: 1.0
Epoch: 283 Loss: 0.056806594133377075 Acc: 1.0
Epoch: 284 Loss: 0.0563981719315052 Acc: 1.0
Epoch: 285 Loss: 0.055994126945734024 Acc: 1.0
Epoch: 286 Loss: 0.055594395846128464 Acc: 1.0
Epoch: 287 Loss: 0.055198948830366135 Acc: 1.0
Epoch: 288 Loss: 0.05480771139264107 Acc: 1.0
Epoch: 289 Loss: 0.05442064255475998 Acc: 1.0
Epoch: 290 Loss: 0.054037682712078094 Acc: 1.0
Epoch: 291 Loss: 0.05365878343582153 Acc: 1.0
Epoch: 292 Loss: 0.053283900022506714 Acc: 1.0
Epoch: 293 Loss: 0.05291297659277916 Acc: 1.0
Epoch: 294 Loss: 0.05254595726728439 Acc: 1.0
Epoch: 295 Loss: 0.05218280851840973 Acc: 1.0
Epoch: 296 Loss: 0.05182347074151039 Acc: 1.0
Epoch: 297 Loss: 0.0514679029583931 Acc: 1.0
Epoch: 298 Loss: 0.05111604928970337 Acc: 1.0
Epoch: 299 Loss: 0.05076787248253822 Acc: 1.0
Epoch: 300 Loss: 0.05042332410812378 Acc: 1.0
Epoch: 301 Loss: 0.05008235201239586 Acc: 1.0
Epoch: 302 Loss: 0.04974493011832237 Acc: 1.0
Epoch: 303 Loss: 0.04941098392009735 Acc: 1.0
Epoch: 304 Loss: 0.0490805022418499 Acc: 1.0
Epoch: 305 Loss: 0.04875342547893524 Acc: 1.0
Epoch: 306 Loss: 0.0484297089278698 Acc: 1.0
Epoch: 307 Loss: 0.04810931533575058 Acc: 1.0
Epoch: 308 Loss: 0.04779219999909401 Acc: 1.0
Epoch: 309 Loss: 0.0474783293902874 Acc: 1.0
Epoch: 310 Loss: 0.047167662531137466 Acc: 1.0
Epoch: 311 Loss: 0.046860143542289734 Acc: 1.0
Epoch: 312 Loss: 0.04655575752258301 Acc: 1.0
Epoch: 313 Loss: 0.04625445604324341 Acc: 1.0
Epoch: 314 Loss: 0.045956194400787354 Acc: 1.0
Epoch: 315 Loss: 0.04566092789173126 Acc: 1.0
Epoch: 316 Loss: 0.045368634164333344 Acc: 1.0
Epoch: 317 Loss: 0.045079272240400314 Acc: 1.0
Epoch: 318 Loss: 0.04479281231760979 Acc: 1.0
Epoch: 319 Loss: 0.04450920596718788 Acc: 1.0
Epoch: 320 Loss: 0.04422843083739281 Acc: 1.0
Epoch: 321 Loss: 0.043950434774160385 Acc: 1.0
Epoch: 322 Loss: 0.04367521032691002 Acc: 1.0
Epoch: 323 Loss: 0.04340269789099693 Acc: 1.0
Epoch: 324 Loss: 0.04313287511467934 Acc: 1.0
Epoch: 325 Loss: 0.04286570101976395 Acc: 1.0
Epoch: 326 Loss: 0.042601145803928375 Acc: 1.0
Epoch: 327 Loss: 0.04233918339014053 Acc: 1.0
Epoch: 328 Loss: 0.04207979142665863 Acc: 1.0
Epoch: 329 Loss: 0.04182291030883789 Acc: 1.0
Epoch: 330 Loss: 0.04156852886080742 Acc: 1.0
Epoch: 331 Loss: 0.04131660982966423 Acc: 1.0
Epoch: 332 Loss: 0.041067130863666534 Acc: 1.0
Epoch: 333 Loss: 0.040820054709911346 Acc: 1.0
Epoch: 334 Loss: 0.040575359016656876 Acc: 1.0
Epoch: 335 Loss: 0.04033299535512924 Acc: 1.0
Epoch: 336 Loss: 0.04009297117590904 Acc: 1.0
Epoch: 337 Loss: 0.0398552268743515 Acc: 1.0
Epoch: 338 Loss: 0.03961974009871483 Acc: 1.0
Epoch: 339 Loss: 0.03938649222254753 Acc: 1.0
Epoch: 340 Loss: 0.03915545344352722 Acc: 1.0
Epoch: 341 Loss: 0.03892659395933151 Acc: 1.0
Epoch: 342 Loss: 0.03869989141821861 Acc: 1.0
Epoch: 343 Loss: 0.03847532346844673 Acc: 1.0
Epoch: 344 Loss: 0.038252852857112885 Acc: 1.0
Epoch: 345 Loss: 0.03803245350718498 Acc: 1.0
Epoch: 346 Loss: 0.03781411424279213 Acc: 1.0
Epoch: 347 Loss: 0.03759780898690224 Acc: 1.0
Epoch: 348 Loss: 0.03738350048661232 Acc: 1.0
Epoch: 349 Loss: 0.037171173840761185 Acc: 1.0
Epoch: 350 Loss: 0.03696080297231674 Acc: 1.0
Epoch: 351 Loss: 0.036752376705408096 Acc: 1.0
Epoch: 352 Loss: 0.036545850336551666 Acc: 1.0
Epoch: 353 Loss: 0.036341216415166855 Acc: 1.0
Epoch: 354 Loss: 0.036138441413640976 Acc: 1.0
Epoch: 355 Loss: 0.03593752160668373 Acc: 1.0
Epoch: 356 Loss: 0.03573841229081154 Acc: 1.0
Epoch: 357 Loss: 0.0355411097407341 Acc: 1.0
Epoch: 358 Loss: 0.03534558415412903 Acc: 1.0
Epoch: 359 Loss: 0.03515181690454483 Acc: 1.0
Epoch: 360 Loss: 0.034959785640239716 Acc: 1.0
Epoch: 361 Loss: 0.03476947546005249 Acc: 1.0
Epoch: 362 Loss: 0.03458086773753166 Acc: 1.0
Epoch: 363 Loss: 0.03439393639564514 Acc: 1.0
Epoch: 364 Loss: 0.03420865908265114 Acc: 1.0
Epoch: 365 Loss: 0.03402501344680786 Acc: 1.0
Epoch: 366 Loss: 0.03384300321340561 Acc: 1.0
Epoch: 367 Loss: 0.0336625836789608 Acc: 1.0
Epoch: 368 Loss: 0.033483751118183136 Acc: 1.0
Epoch: 369 Loss: 0.03330647572875023 Acc: 1.0
Epoch: 370 Loss: 0.03313075751066208 Acc: 1.0
Epoch: 371 Loss: 0.0329565592110157 Acc: 1.0
Epoch: 372 Loss: 0.0327838771045208 Acc: 1.0
Epoch: 373 Loss: 0.03261268883943558 Acc: 1.0
Epoch: 374 Loss: 0.03244297578930855 Acc: 1.0
Epoch: 375 Loss: 0.032274726778268814 Acc: 1.0
Epoch: 376 Loss: 0.032107915729284286 Acc: 1.0
Epoch: 377 Loss: 0.031942542642354965 Acc: 1.0
Epoch: 378 Loss: 0.031778573989868164 Acc: 1.0
Epoch: 379 Loss: 0.031616002321243286 Acc: 1.0
Epoch: 380 Loss: 0.03145480155944824 Acc: 1.0
Epoch: 381 Loss: 0.03129497915506363 Acc: 1.0
Epoch: 382 Loss: 0.031136494129896164 Acc: 1.0
Epoch: 383 Loss: 0.030979346483945847 Acc: 1.0
Epoch: 384 Loss: 0.030823517590761185 Acc: 1.0
Epoch: 385 Loss: 0.030668988823890686 Acc: 1.0
Epoch: 386 Loss: 0.030515752732753754 Acc: 1.0
Epoch: 387 Loss: 0.030363788828253746 Acc: 1.0
Epoch: 388 Loss: 0.030213089659810066 Acc: 1.0
Epoch: 389 Loss: 0.030063634738326073 Acc: 1.0
Epoch: 390 Loss: 0.029915418475866318 Acc: 1.0
Epoch: 391 Loss: 0.02976842038333416 Acc: 1.0
Epoch: 392 Loss: 0.029622631147503853 Acc: 1.0
Epoch: 393 Loss: 0.029478026553988457 Acc: 1.0
Epoch: 394 Loss: 0.02933460846543312 Acc: 1.0
Epoch: 395 Loss: 0.029192356392741203 Acc: 1.0
Epoch: 396 Loss: 0.02905125543475151 Acc: 1.0
Epoch: 397 Loss: 0.028911296278238297 Acc: 1.0
Epoch: 398 Loss: 0.028772473335266113 Acc: 1.0
Epoch: 399 Loss: 0.02863476239144802 Acc: 1.0
Epoch: 400 Loss: 0.028498154133558273 Acc: 1.0
Epoch: 401 Loss: 0.02836264669895172 Acc: 1.0
Epoch: 402 Loss: 0.028228215873241425 Acc: 1.0
Epoch: 403 Loss: 0.028094854205846786 Acc: 1.0
Epoch: 404 Loss: 0.02796255238354206 Acc: 1.0
Epoch: 405 Loss: 0.0278313010931015 Acc: 1.0
Epoch: 406 Loss: 0.027701083570718765 Acc: 1.0
Epoch: 407 Loss: 0.027571888640522957 Acc: 1.0
Epoch: 408 Loss: 0.02744371071457863 Acc: 1.0
Epoch: 409 Loss: 0.027316533029079437 Acc: 1.0
Epoch: 410 Loss: 0.027190357446670532 Acc: 1.0
Epoch: 411 Loss: 0.027065154165029526 Acc: 1.0
Epoch: 412 Loss: 0.026940928772091866 Acc: 1.0
Epoch: 413 Loss: 0.02681766077876091 Acc: 1.0
Epoch: 414 Loss: 0.02669535204768181 Acc: 1.0
Epoch: 415 Loss: 0.02657397650182247 Acc: 1.0
Epoch: 416 Loss: 0.0264535341411829 Acc: 1.0
Epoch: 417 Loss: 0.026334023103117943 Acc: 1.0
Epoch: 418 Loss: 0.02621541917324066 Acc: 1.0
Epoch: 419 Loss: 0.026097716763615608 Acc: 1.0
Epoch: 420 Loss: 0.025980906561017036 Acc: 1.0
Epoch: 421 Loss: 0.025864986702799797 Acc: 1.0
Epoch: 422 Loss: 0.025749940425157547 Acc: 1.0
Epoch: 423 Loss: 0.02563575655221939 Acc: 1.0
Epoch: 424 Loss: 0.025522436946630478 Acc: 1.0
Epoch: 425 Loss: 0.025409964844584465 Acc: 1.0
Epoch: 426 Loss: 0.025298327207565308 Acc: 1.0
Epoch: 427 Loss: 0.025187531486153603 Acc: 1.0
Epoch: 428 Loss: 0.02507755346596241 Acc: 1.0
Epoch: 429 Loss: 0.02496838942170143 Acc: 1.0
Epoch: 430 Loss: 0.024860035628080368 Acc: 1.0
Epoch: 431 Loss: 0.024752484634518623 Acc: 1.0
Epoch: 432 Loss: 0.024645715951919556 Acc: 1.0
Epoch: 433 Loss: 0.02453973889350891 Acc: 1.0
Epoch: 434 Loss: 0.0244345273822546 Acc: 1.0
Epoch: 435 Loss: 0.02433009073138237 Acc: 1.0
Epoch: 436 Loss: 0.024226410314440727 Acc: 1.0
Epoch: 437 Loss: 0.024123484268784523 Acc: 1.0
Epoch: 438 Loss: 0.024021297693252563 Acc: 1.0
Epoch: 439 Loss: 0.023919852450489998 Acc: 1.0
Epoch: 440 Loss: 0.02381914108991623 Acc: 1.0
Epoch: 441 Loss: 0.023719146847724915 Acc: 1.0
Epoch: 442 Loss: 0.023619869723916054 Acc: 1.0
Epoch: 443 Loss: 0.0235213004052639 Acc: 1.0
Epoch: 444 Loss: 0.02342342957854271 Acc: 1.0
Epoch: 445 Loss: 0.023326264694333076 Acc: 1.0
Epoch: 446 Loss: 0.023229777812957764 Acc: 1.0
Epoch: 447 Loss: 0.023133980110287666 Acc: 1.0
Epoch: 448 Loss: 0.02303885854780674 Acc: 1.0
Epoch: 449 Loss: 0.02294440194964409 Acc: 1.0
Epoch: 450 Loss: 0.022850608453154564 Acc: 1.0
Epoch: 451 Loss: 0.02275746315717697 Acc: 1.0
Epoch: 452 Loss: 0.022664977237582207 Acc: 1.0
Epoch: 453 Loss: 0.02257312834262848 Acc: 1.0
Epoch: 454 Loss: 0.022481918334960938 Acc: 1.0
Epoch: 455 Loss: 0.022391345351934433 Acc: 1.0
Epoch: 456 Loss: 0.022301387041807175 Acc: 1.0
Epoch: 457 Loss: 0.02221205085515976 Acc: 1.0
Epoch: 458 Loss: 0.02212333120405674 Acc: 1.0
Epoch: 459 Loss: 0.02203521691262722 Acc: 1.0
Epoch: 460 Loss: 0.021947702392935753 Acc: 1.0
Epoch: 461 Loss: 0.021860789507627487 Acc: 1.0
Epoch: 462 Loss: 0.02177446335554123 Acc: 1.0
Epoch: 463 Loss: 0.02168872207403183 Acc: 1.0
Epoch: 464 Loss: 0.02160356380045414 Acc: 1.0
Epoch: 465 Loss: 0.021518975496292114 Acc: 1.0
Epoch: 466 Loss: 0.021434959024190903 Acc: 1.0
Epoch: 467 Loss: 0.02135150320827961 Acc: 1.0
Epoch: 468 Loss: 0.021268609911203384 Acc: 1.0
Epoch: 469 Loss: 0.021186266094446182 Acc: 1.0
Epoch: 470 Loss: 0.021104469895362854 Acc: 1.0
Epoch: 471 Loss: 0.021023215726017952 Acc: 1.0
Epoch: 472 Loss: 0.020942501723766327 Acc: 1.0
Epoch: 473 Loss: 0.02086232416331768 Acc: 1.0
Epoch: 474 Loss: 0.020782670006155968 Acc: 1.0
Epoch: 475 Loss: 0.020703542977571487 Acc: 1.0
Epoch: 476 Loss: 0.020624930039048195 Acc: 1.0
Epoch: 477 Loss: 0.02054683305323124 Acc: 1.0
Epoch: 478 Loss: 0.020469246432185173 Acc: 1.0
Epoch: 479 Loss: 0.02039216458797455 Acc: 1.0
Epoch: 480 Loss: 0.020315583795309067 Acc: 1.0
Epoch: 481 Loss: 0.02023949660360813 Acc: 1.0
Epoch: 482 Loss: 0.02016390673816204 Acc: 1.0
Epoch: 483 Loss: 0.020088791847229004 Acc: 1.0
Epoch: 484 Loss: 0.020014168694615364 Acc: 1.0
Epoch: 485 Loss: 0.019940022379159927 Acc: 1.0
Epoch: 486 Loss: 0.019866356626152992 Acc: 1.0
Epoch: 487 Loss: 0.019793150946497917 Acc: 1.0
Epoch: 488 Loss: 0.0197204127907753 Acc: 1.0
Epoch: 489 Loss: 0.01964813843369484 Acc: 1.0
Epoch: 490 Loss: 0.019576316699385643 Acc: 1.0
Epoch: 491 Loss: 0.019504951313138008 Acc: 1.0
Epoch: 492 Loss: 0.019434038549661636 Acc: 1.0
Epoch: 493 Loss: 0.01936357468366623 Acc: 1.0
Epoch: 494 Loss: 0.019293542951345444 Acc: 1.0
Epoch: 495 Loss: 0.019223947077989578 Acc: 1.0
Epoch: 496 Loss: 0.01915479637682438 Acc: 1.0
Epoch: 497 Loss: 0.019086072221398354 Acc: 1.0
Epoch: 498 Loss: 0.019017772749066353 Acc: 1.0
Epoch: 499 Loss: 0.018949899822473526 Acc: 1.0

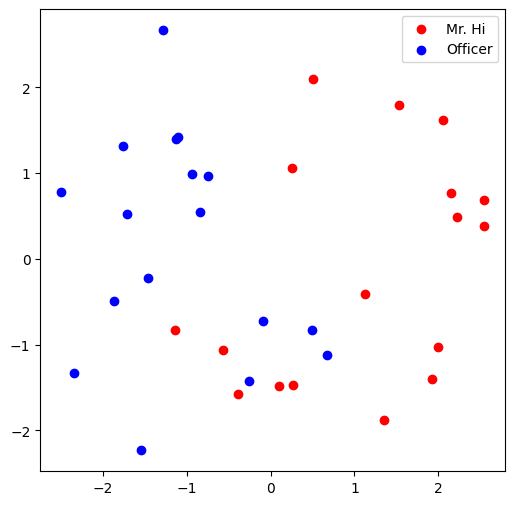
8.4.3. Visualize the final node embeddings

Visualize your final embedding here! You can visually compare the figure with the previous embedding figure. After training, you should oberserve that the two classes are more evidently separated. This is a great sanitity check for your implementation as well.

# Visualize the final learned embedding
visualize_emb(emb)

8.5. Implementing Graph Neural Networks (GNNs)

After learning about PyG’s data handling, it’s time to implement our first Graph Neural Network!

For this, we will use one of the most simple GNN operators, the GCN layer (Kipf et al. (2017)).

PyG implements this layer via GCNConv, which can be executed by passing in the node feature representation x and the COO graph connectivity representation edge_index.

8.5.1. What is the output of a GNN?

The goal of a GNN is to take an input graph \(G = (\mathbb{V}, \mathbb{E})\) where each node \(v_i \in \mathbb{V}\) has an input feature vector \(X_i^{(0)}\). What we want to learn is a function \(f \to \mathbb{V} \times \mathbb{R}^d\), a function that takes in a node and its feature vector, as well as the graph structure, and outputs an embedding, a vector that represents that node in a way that’s useful to our downstream task. Once we’ve mapped nodes and their initial features to their learned embeddings, we can use those embeddings to do a variety of different tasks including node-level, edge-level, or graph-level regression/classification.

In this colab, we want to learn embeddings that will be useful to classify each node into its community.

With this, we are ready to create our first Graph Neural Network by defining our network architecture in a torch.nn.Module class:

import torch
from torch.nn import Linear
from torch_geometric.nn import GCNConv

class GCN(torch.nn.Module):
    def __init__(self):
        super().__init__()
        torch.manual_seed(1234)
        self.conv1 = GCNConv(dataset.num_features, 4)
        self.conv2 = GCNConv(4, 4)
        self.conv3 = GCNConv(4, 2)
        self.classifier = Linear(2, dataset.num_classes)

    def forward(self, x, edge_index):
        h = self.conv1(x, edge_index)
        h = h.tanh()
        h = self.conv2(h, edge_index)
        h = h.tanh()
        h = self.conv3(h, edge_index)
        h = h.tanh()  # Final GNN embedding space.

        # Apply a final (linear) classifier.
        out = self.classifier(h)

        return out, h

model = GCN()
print(model)

GCN(
  (conv1): GCNConv(34, 4)
  (conv2): GCNConv(4, 4)
  (conv3): GCNConv(4, 2)
  (classifier): Linear(in_features=2, out_features=4, bias=True)
)

Here, we first initialize all of our building blocks in __init__ and define the computation flow of our network in forward. We first define and stack three graph convolution layers. Each layer corresponds to aggregating information from each node’s 1-hop neighborhood (its direct neighbors), but when we compose the layers together, we are able to aggregate information from each node’s 3-hop neighborhood (all nodes up to 3 “hops” away).

In addition, the GCNConv layers reduce the node feature dimensionality to \(2\), i.e., \(34 \rightarrow 4 \rightarrow 4 \rightarrow 2\). Each GCNConv layer is enhanced by a tanh non-linearity.

After that, we apply a single linear transformation (torch.nn.Linear) that acts as a classifier to map our nodes to 1 out of the 4 classes/communities.

We return both the output of the final classifier as well as the final node embeddings produced by our GNN. We proceed to initialize our final model via GCN(), and printing our model produces a summary of all its used sub-modules.

model = GCN()

_, h = model(data.x, data.edge_index)
print(f'Embedding shape: {list(h.shape)}')

visualize(h, color=data.y)

Embedding shape: [34, 2]

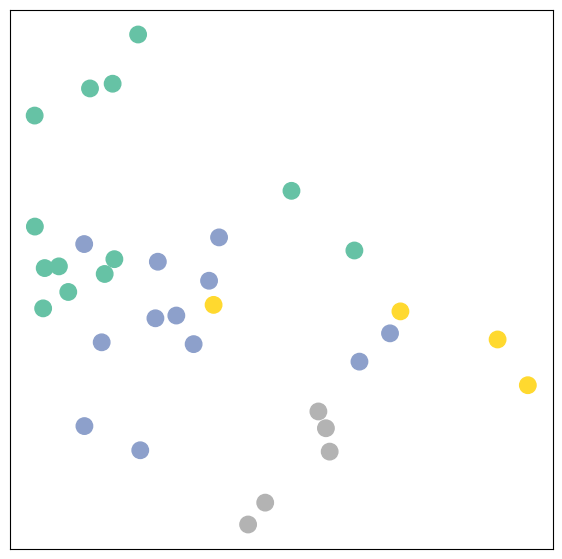
Remarkably, even before training the weights of our model, the model produces an embedding of nodes that closely resembles the community-structure of the graph. Nodes of the same color (community) are already closely clustered together in the embedding space, although the weights of our model are initialized completely at random and we have not yet performed any training so far! This leads to the conclusion that GNNs introduce a strong inductive bias, leading to similar embeddings for nodes that are close to each other in the input graph.

8.5.2. Exercise

8.5.2.1. Question 10: Training GCN on the Karate Club Network! What is the best performance you can receive? Please report both the best loss and accur on gradescope.

But can we do better? Let’s look at an example on how to train our network parameters based on the knowledge of the community assignments of 4 nodes in the graph (one for each community):

Since everything in our model is differentiable and parameterized, we can add some labels, train the model and observe how the embeddings react. Here, we make use of a semi-supervised or transductive learning procedure: We simply train against one node per class, but are allowed to make use of the complete input graph data.

Training our model is very similar to any other PyTorch model. In addition to defining our network architecture, we define a loss critertion (here, CrossEntropyLoss) and initialize a stochastic gradient optimizer (here, Adam). After that, we perform multiple rounds of optimization, where each round consists of a forward and backward pass to compute the gradients of our model parameters w.r.t. to the loss derived from the forward pass. If you are not new to PyTorch, this scheme should appear familar to you. Otherwise, the PyTorch docs provide a good introduction on how to train a neural network in PyTorch.

Note that our semi-supervised learning scenario is achieved by the following line:

loss = criterion(out[data.train_mask], data.y[data.train_mask])

While we compute node embeddings for all of our nodes, we only make use of the training nodes for computing the loss. Here, this is implemented by filtering the output of the classifier out and ground-truth labels data.y to only contain the nodes in the train_mask.

Let us now start training and see how our node embeddings evolve over time (best experienced by explicitely running the code):

import time
from IPython.display import Javascript  # Restrict height of output cell.
display(Javascript('''google.colab.output.setIframeHeight(0, true, {maxHeight: 430})'''))

model = GCN()
criterion = torch.nn.CrossEntropyLoss()  # Define loss criterion.
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)  # Define optimizer.

def train(data):
    optimizer.zero_grad()  # Clear gradients.
    out, h = model(data.x, data.edge_index)  # Perform a single forward pass.
    loss = criterion(out[data.train_mask], data.y[data.train_mask])  # Compute the loss solely based on the training nodes.
    loss.backward()  # Derive gradients.
    optimizer.step()  # Update parameters based on gradients.

    accuracy = {}

    # Calculate training accuracy on our four examples
    predicted_classes = torch.argmax(out[data.train_mask], axis=1) # [0.6, 0.2, 0.7, 0.1] -> 2
    target_classes = data.y[data.train_mask]
    accuracy['train'] = torch.mean(
        torch.where(predicted_classes == target_classes, 1, 0).float())

    ############# Your code here ############
    # Calculate validation accuracy on the whole graph

    #########################################

    return loss, h, accuracy

for epoch in range(500):
    loss, h, accuracy = train(data)
    # Visualize the node embeddings every 10 epochs
    if epoch % 10 == 0:
        visualize(h, color=data.y, epoch=epoch, loss=loss, accuracy=accuracy)
        time.sleep(0.3)

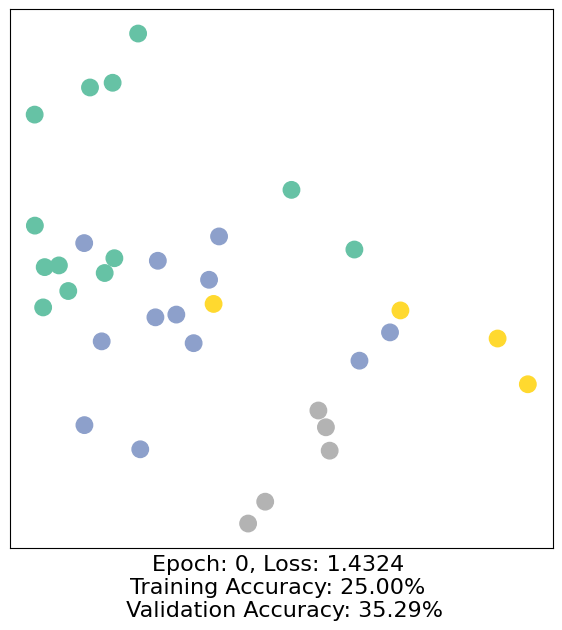
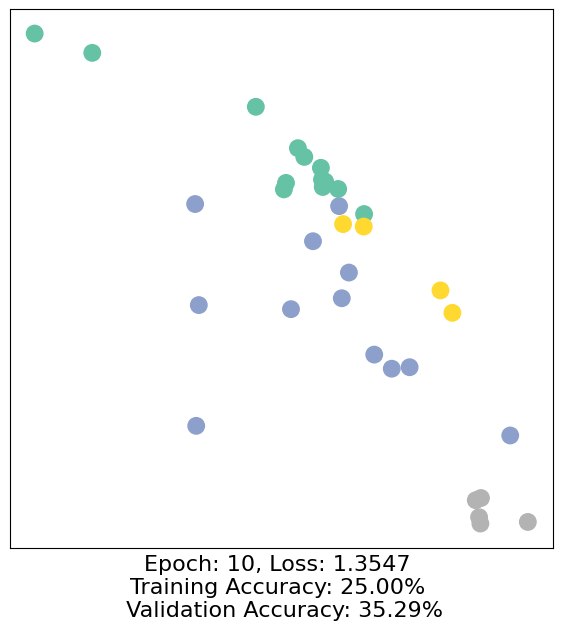
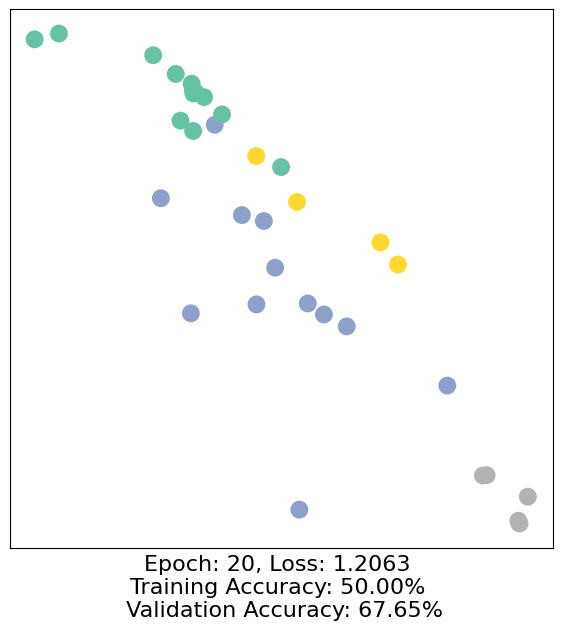
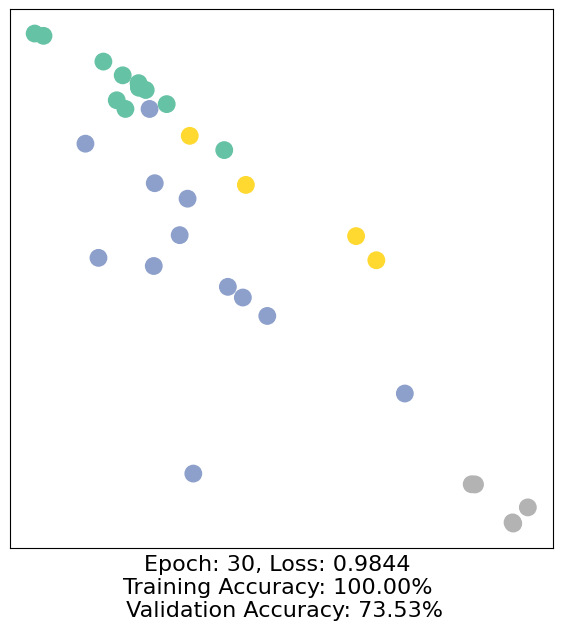
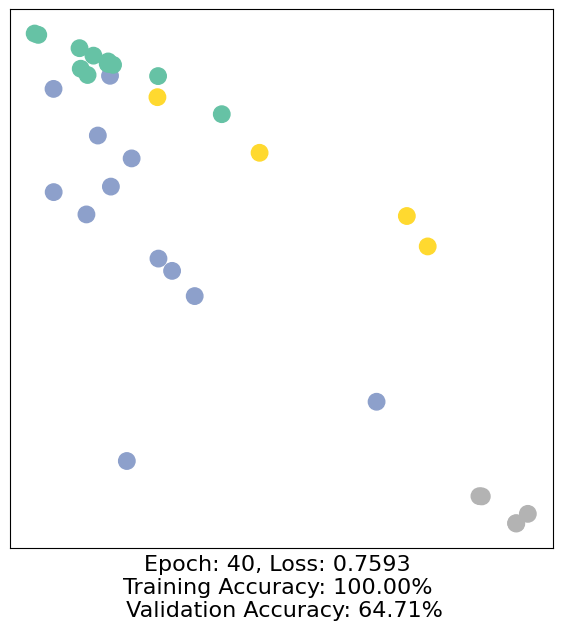
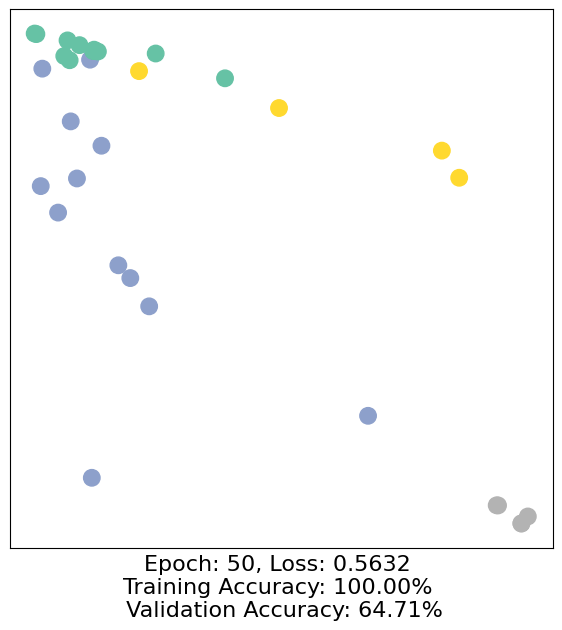
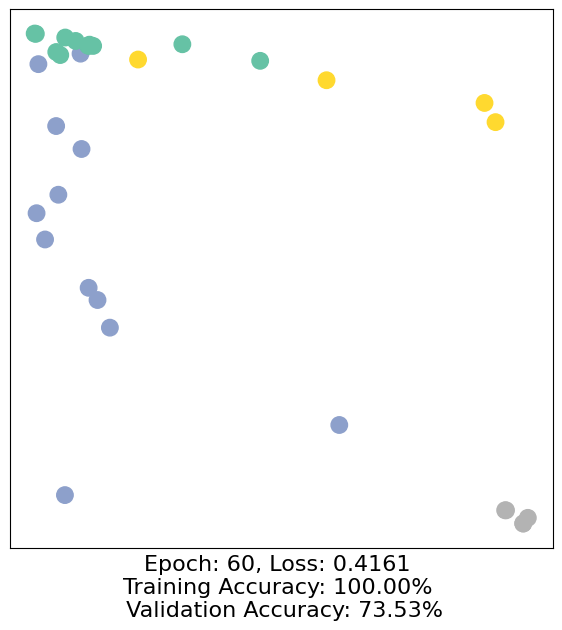
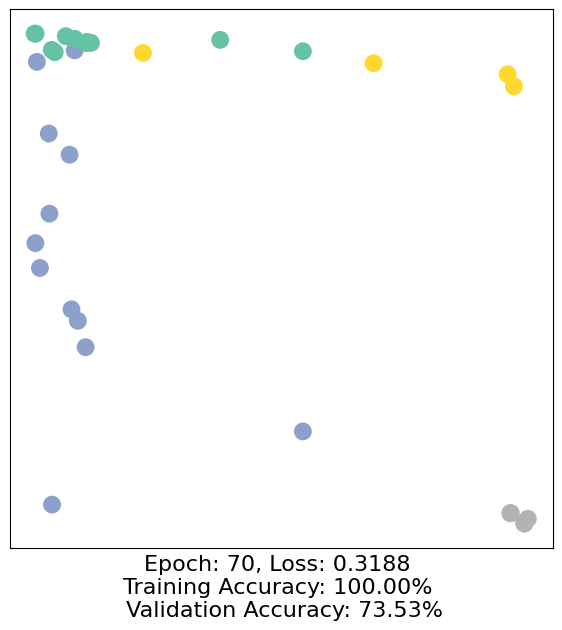
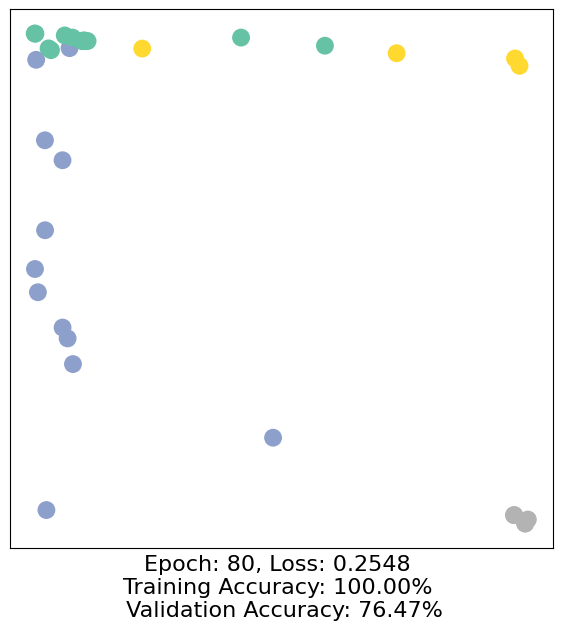
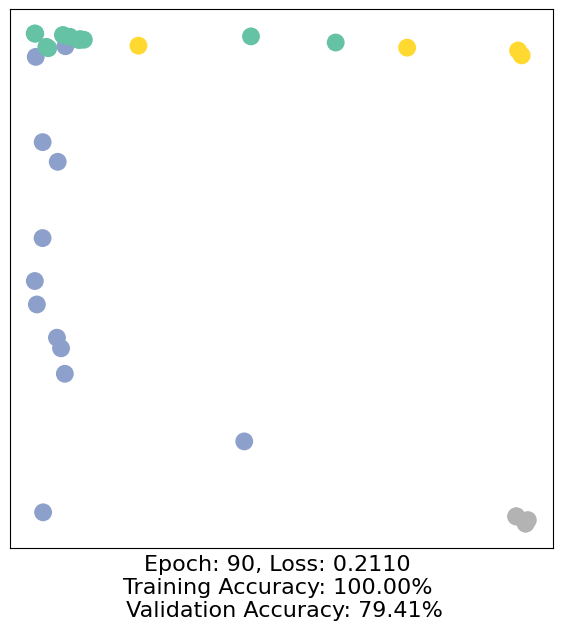
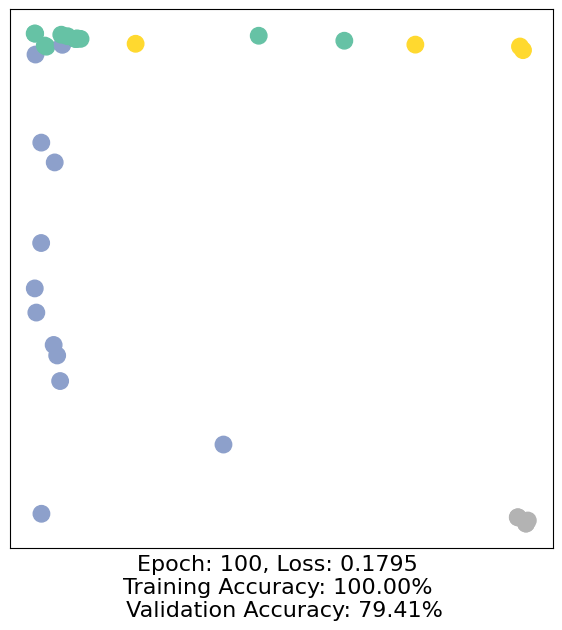
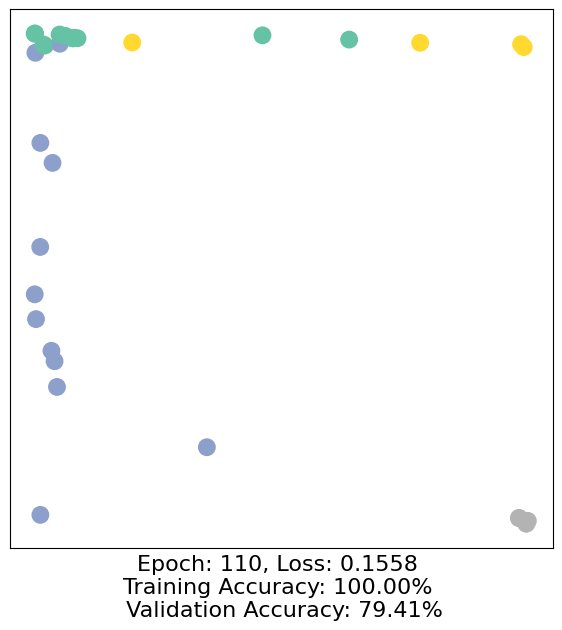
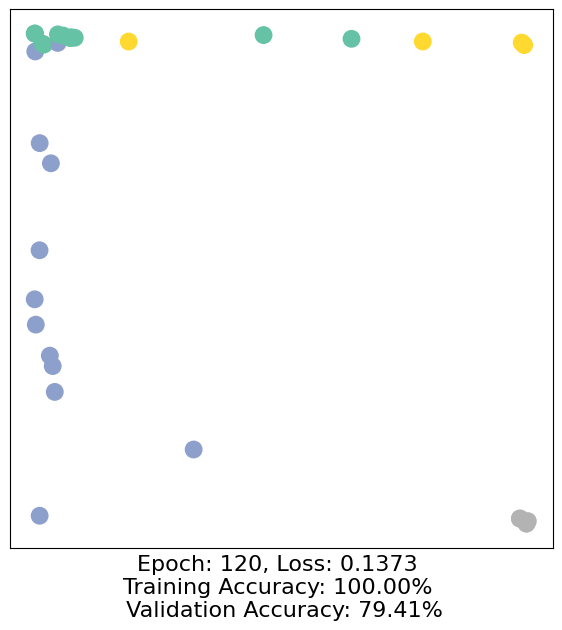
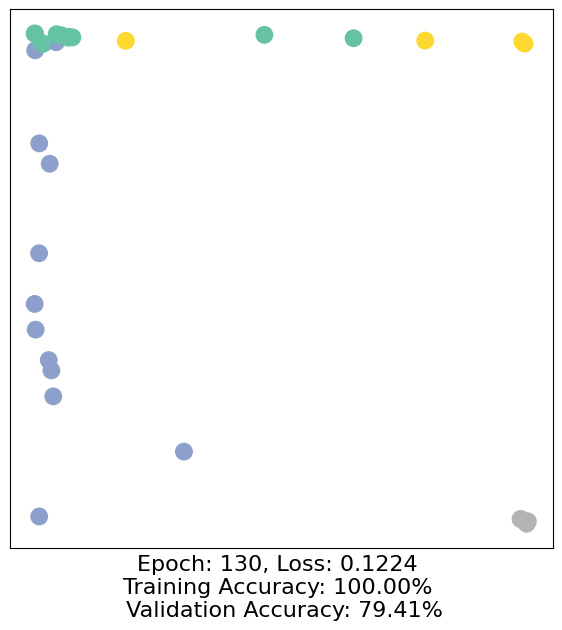
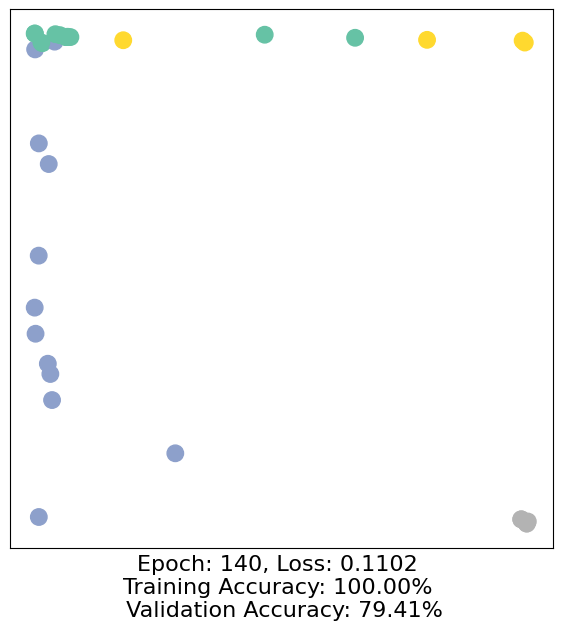
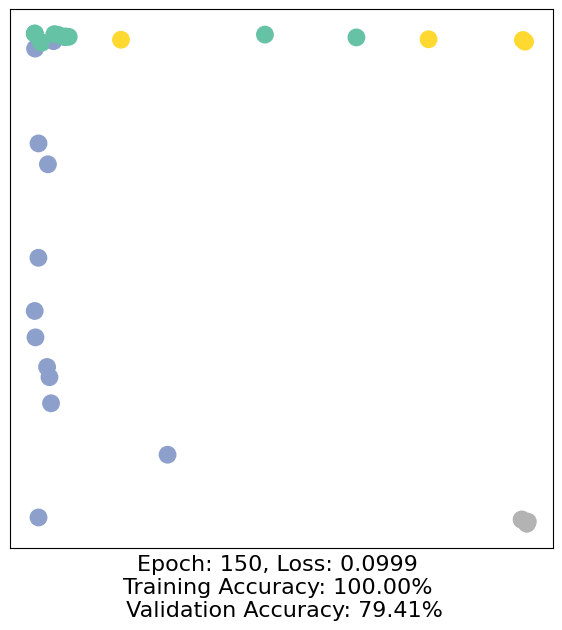
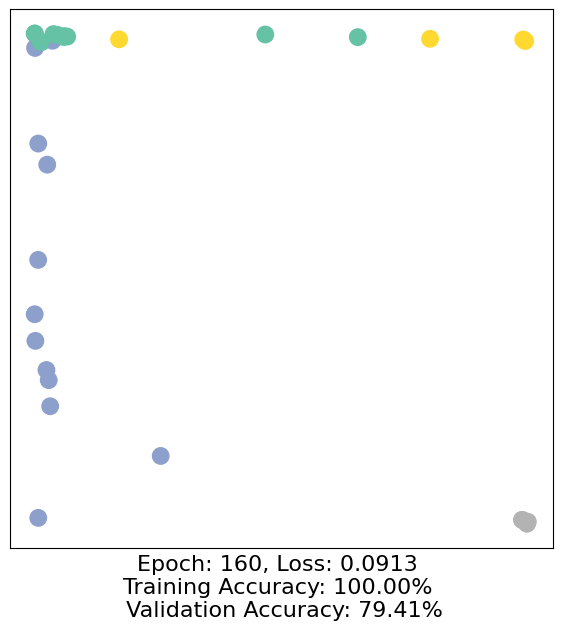
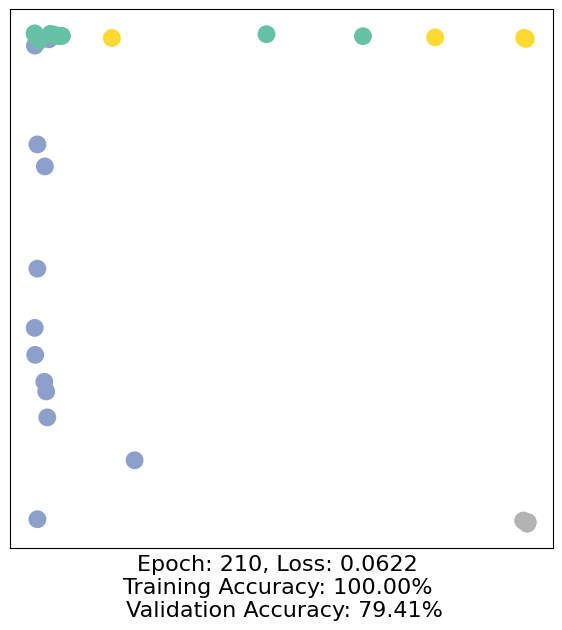
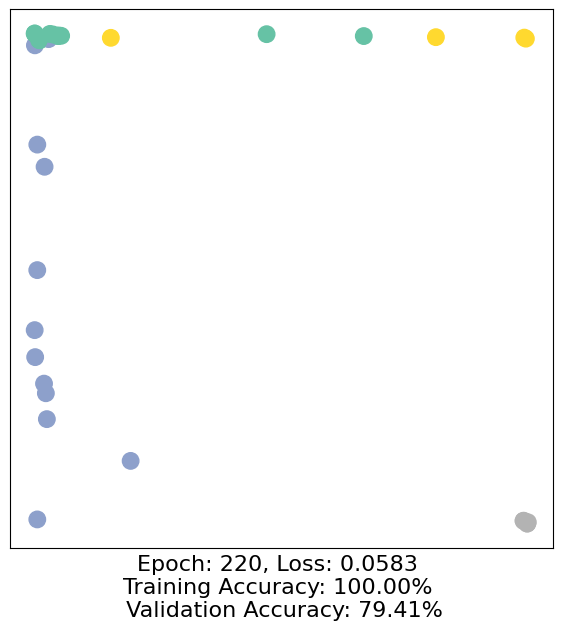
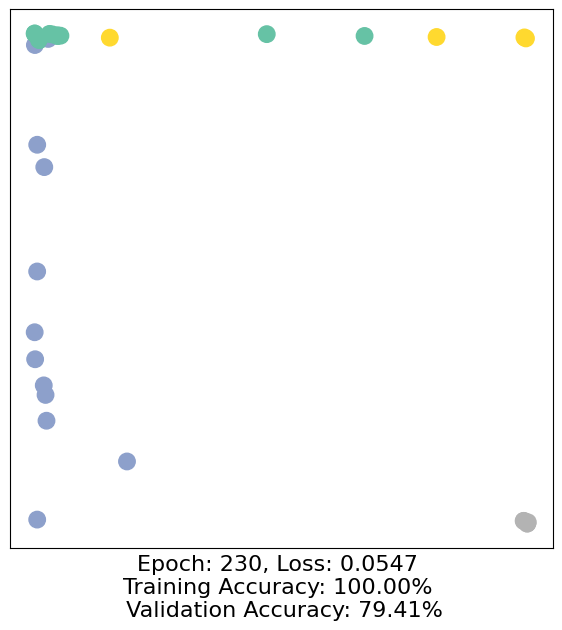
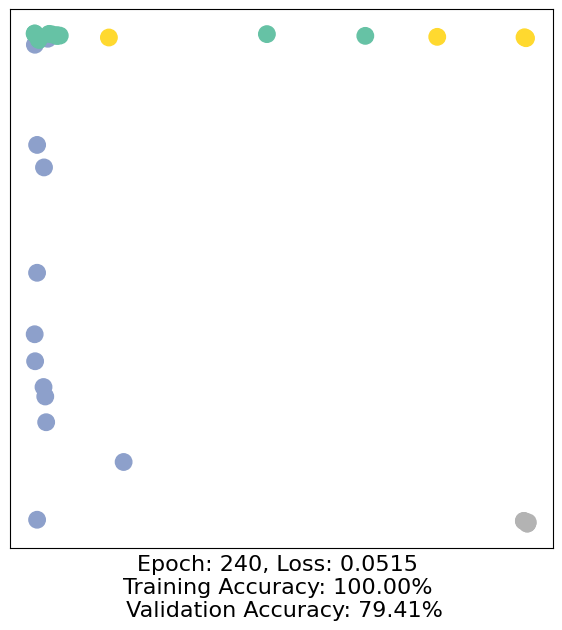
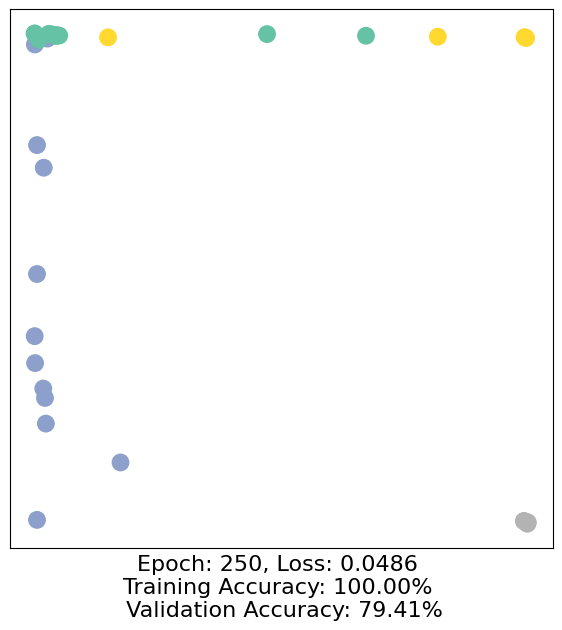
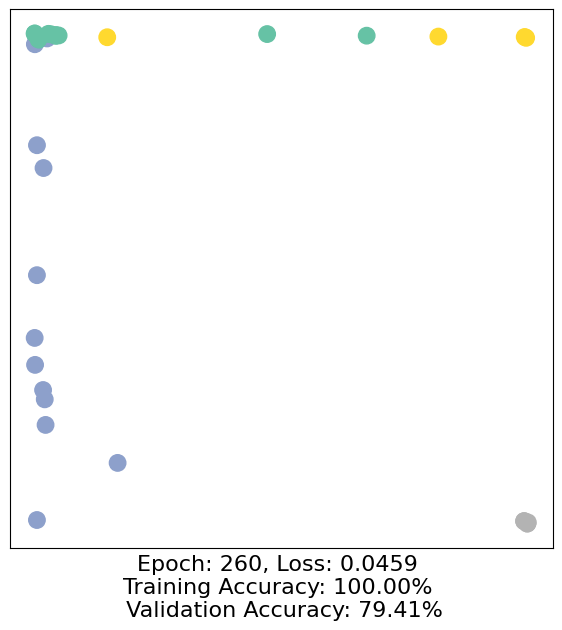
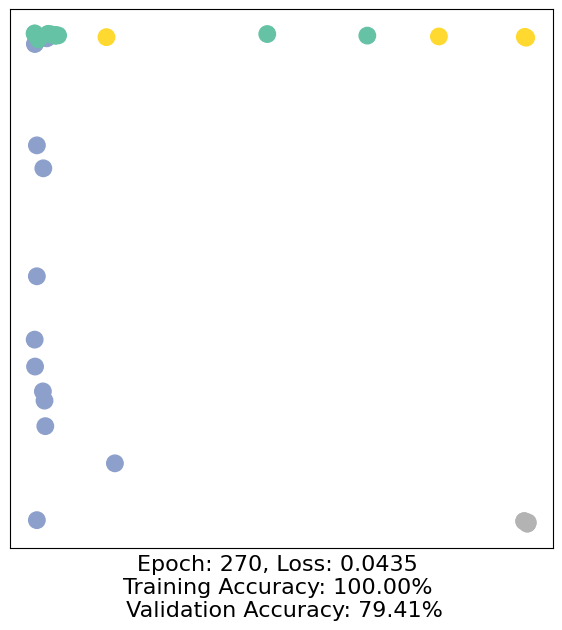
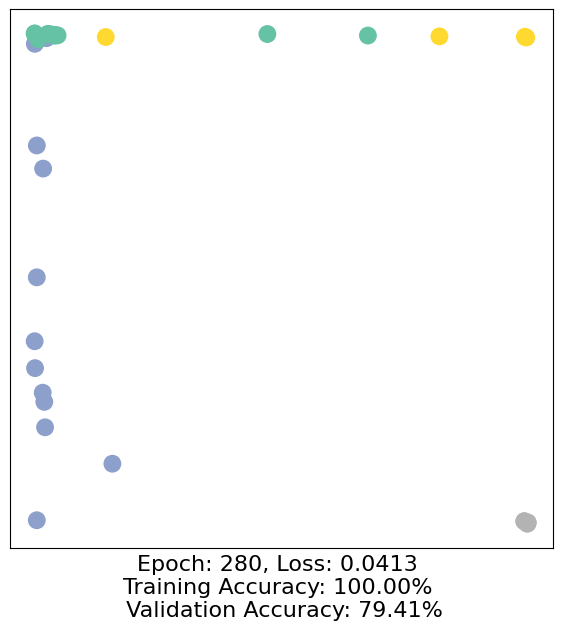
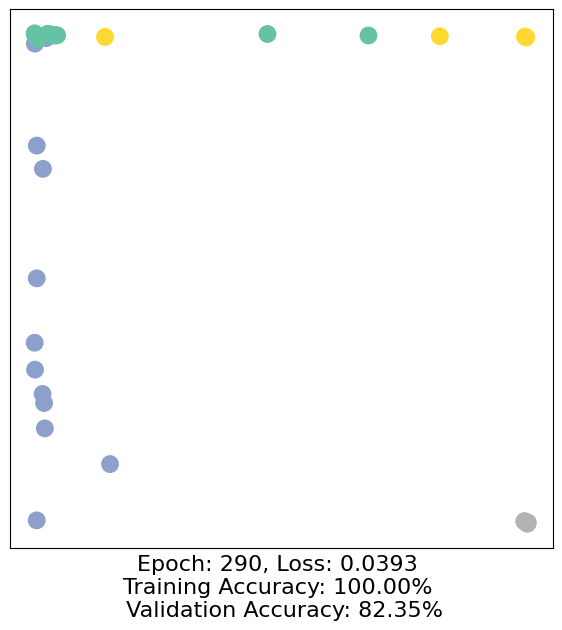
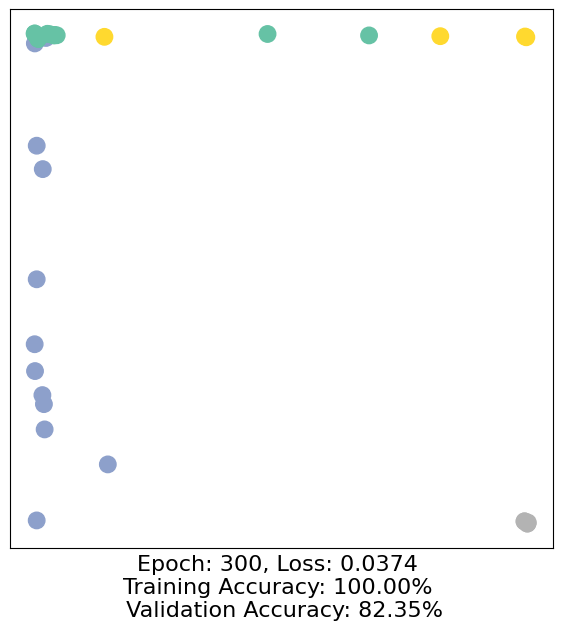
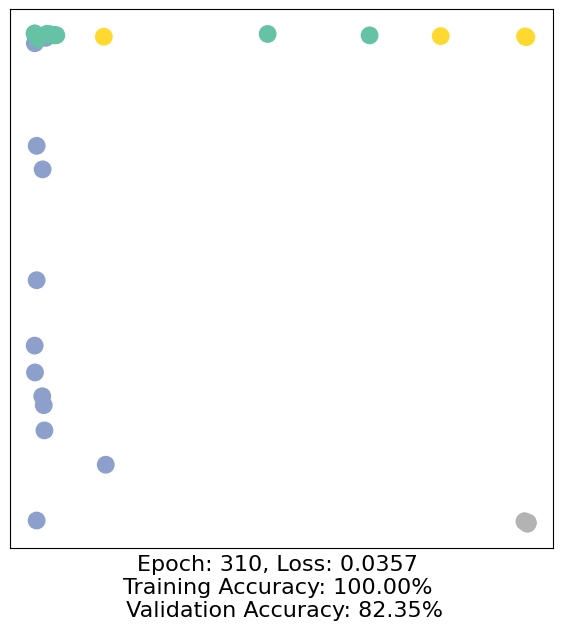
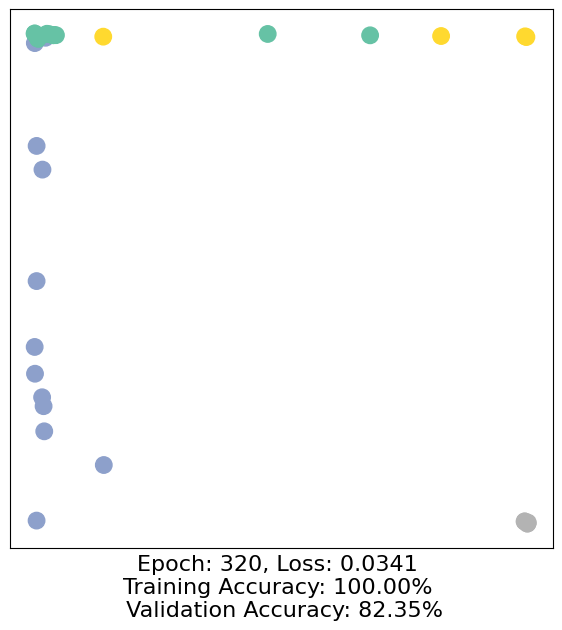
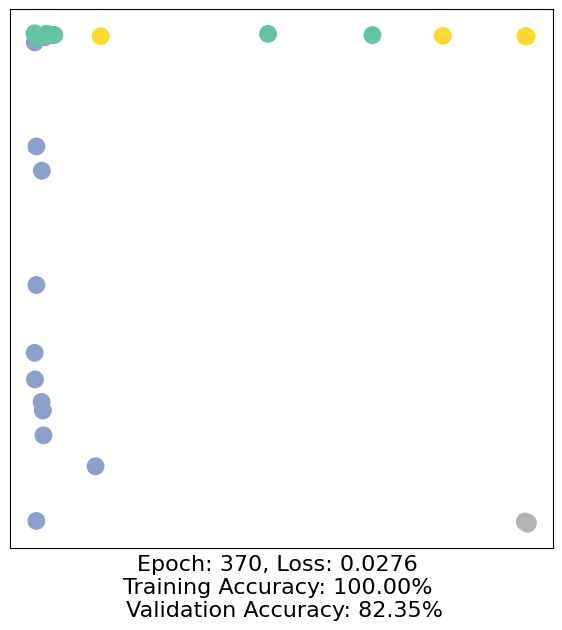
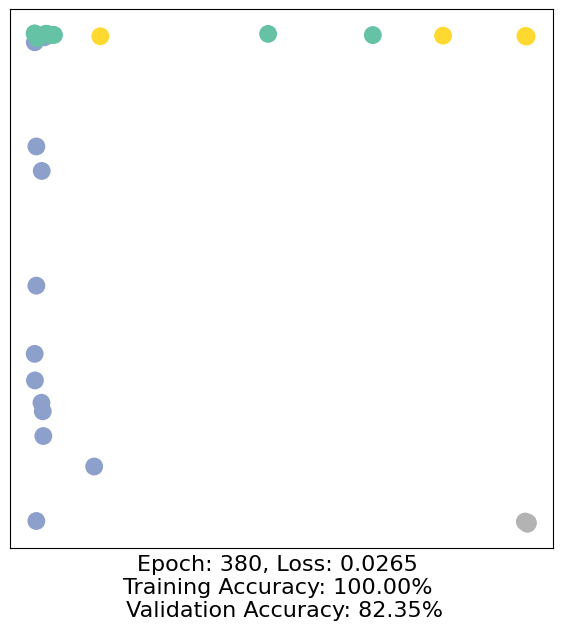
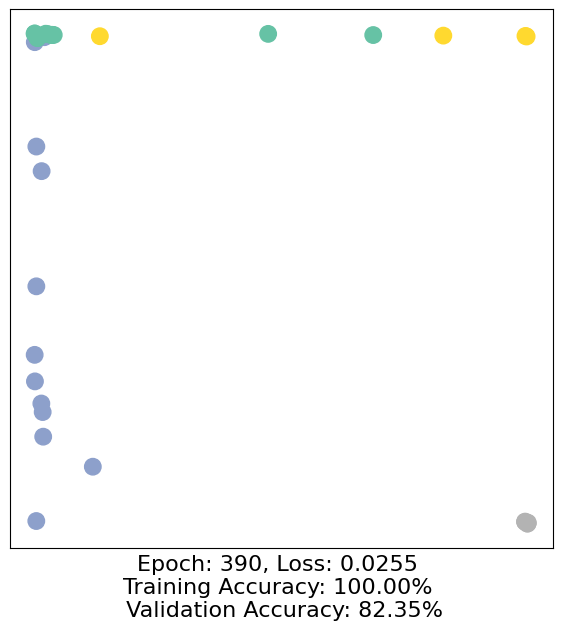
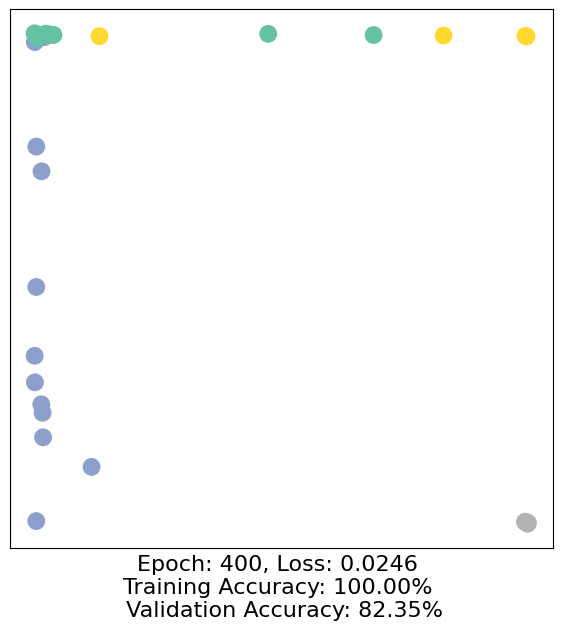
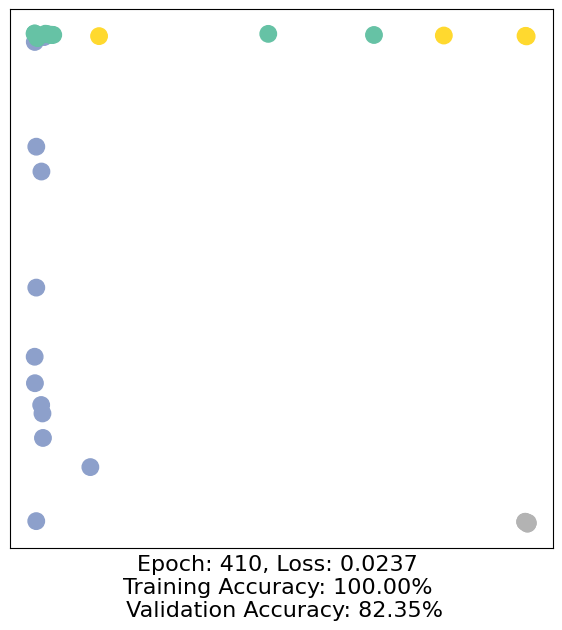
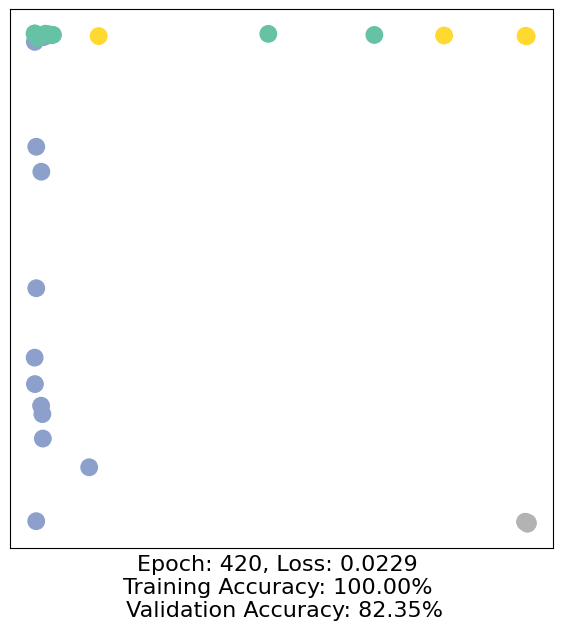
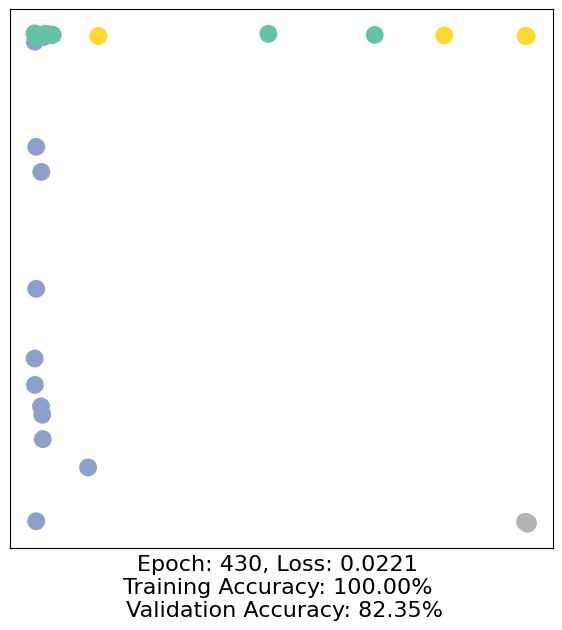
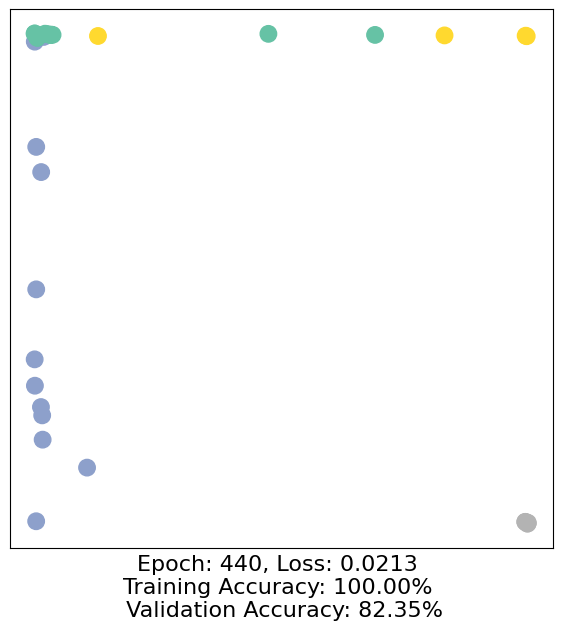
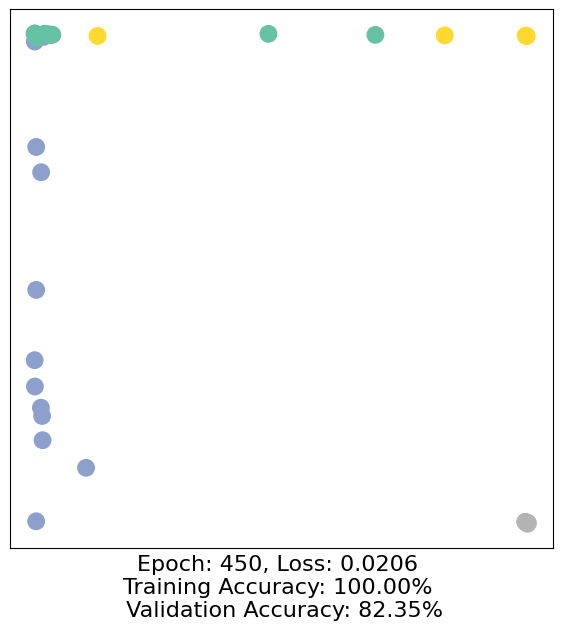
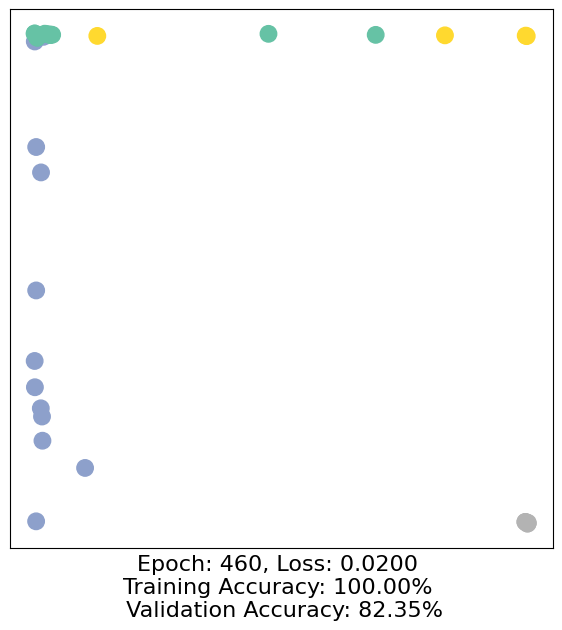
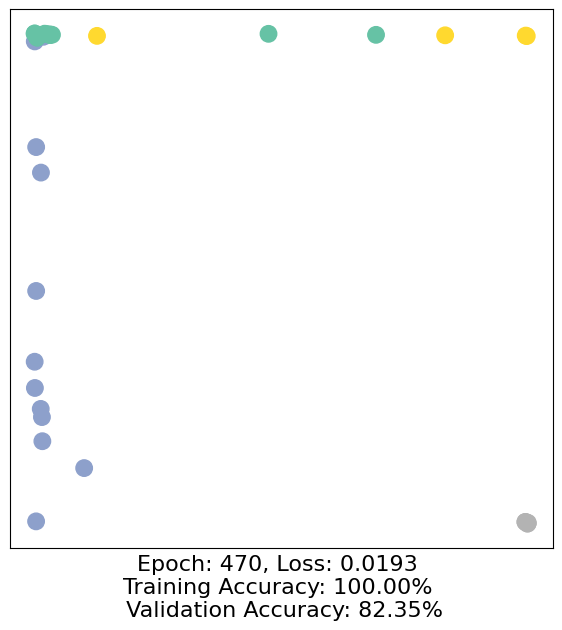
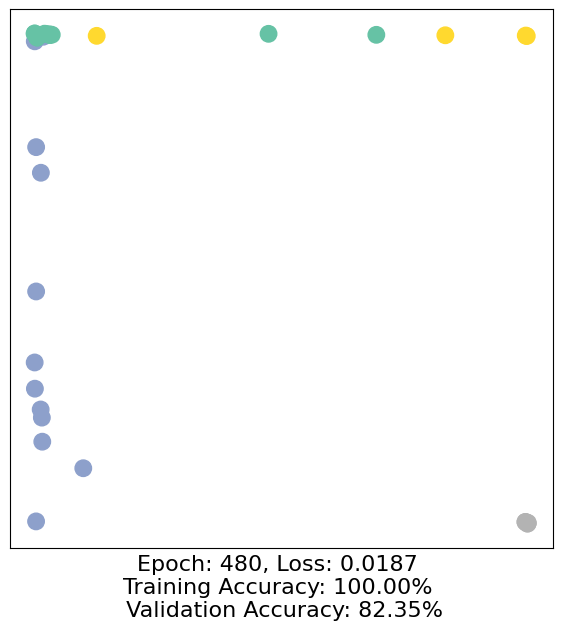
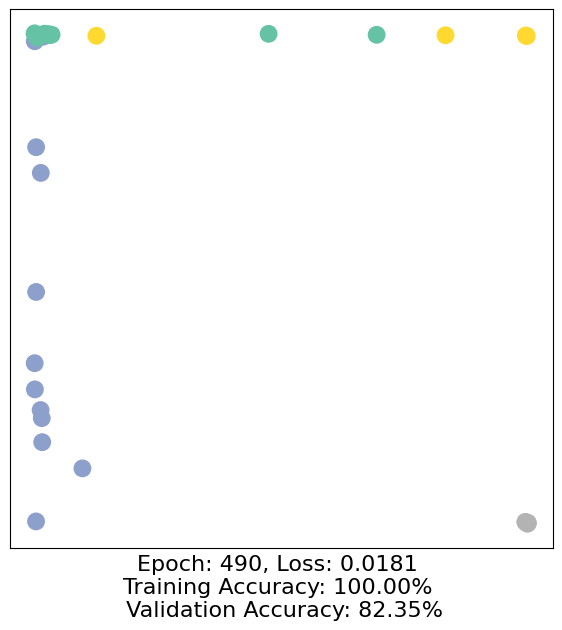
As one can see, our 3-layer GCN model manages to separate the communities pretty well and classify most of the nodes correctly.

Furthermore, we did this all with a few lines of code, thanks to the PyTorch Geometric library which helped us out with data handling and GNN implementations.